Introducere în gruparea ierarhică
- Recent, unul dintre clienții noștri a solicitat echipei noastre să aducă o listă de segmente cu o ordine de importanță în interiorul clienților lor, pentru a le viza să franchizeze unul dintre produsele lor recent lansate. În mod evident, doar segmentarea clienților folosind clustering parțial (k-means, c-fuzzy) nu va scoate la iveală ordinea importanței, acolo este clusteringul ierarhic.
- Gruparea ierarhică separă datele în grupuri diferite pe baza unor măsuri de asemănare cunoscute sub denumirea de clustere, care vizează în esență construirea ierarhiei între clustere. Practic, este învățare nesupravegheată și alegerea atributelor pentru a măsura similaritatea este specifică aplicației.
Clusterul Ierarhiei datelor
- Clustering aglomerativ
- Clustering diviziv
Să luăm un exemplu de date, note obținute de 5 elevi pentru a le grupa pentru o competiție viitoare.
| Student | Marks |
| A | 10 |
| B | 7 |
| C | 28 |
| D | 20 |
| E | 35s |
1. Clustering aglomerativ
- Pentru a începe, considerăm fiecare punct / element individual aici ca pondere și continuăm să unim punctele / elementele similare pentru a forma un nou cluster la noul nivel până când rămânem cu un singur cluster este o abordare de jos în sus.
- O singură legătură și o legătură completă sunt două exemple populare de grupări aglomerative. În afară de această legătură medie și legătură Centroid. Într-o singură legătură, unim în fiecare pas cele două grupuri, ale căror doi membri cei mai apropiați au cea mai mică distanță. În legătură completă, îmbinăm membrii distanței cele mai mici care oferă cea mai mică distanță maximă în pereche.
- Matricea de proximitate, este nucleul pentru efectuarea grupărilor ierarhice, care oferă distanța dintre fiecare punct.
- Să facem matrice de proximitate pentru datele noastre date în tabel, deoarece calculăm distanța dintre fiecare punct cu alte puncte, aceasta va fi o matrice asimetrică de formă n × n, în cazul nostru 5 × 5 matrici.
O metodă populară pentru calculele distanței sunt:
- Distanța euclidiană (pătrat)
dist((x, y), (a, b)) = √(x - a)² + (y - b)²
- Distanța Manhattan
dist((x, y), (a, b)) =|x−c|+|y−d|
Distanța euclidiană este cea mai frecvent utilizată, vom folosi aceeași aici și vom merge cu o legătură complexă.
| Student (Clustere) | A | B | C | D | E |
| A | 0 | 3 | 18 | 10 | 25 |
| B | 3 | 0 | 21 | 13 | 28 |
| C | 18 | 21 | 0 | 8 | 7 |
| D | 10 | 13 | 8 | 0 | 15 |
| E | 25 | 28 | 7 | 15 | 0 |
Elementele diagonale ale matricei de proximitate vor fi întotdeauna 0, deoarece distanța dintre punctul cu același punct va fi întotdeauna 0, prin urmare, elementele diagonale sunt scutite de considerare pentru grupare.
Aici, în iterația 1, cea mai mică distanță este de 3, prin urmare, unim A și B pentru a forma un cluster, formând din nou o matrice de proximitate cu cluster (A, B) luând (A, B) punctul de cluster ca 10, adică maxim de ( 7, 10) o matrice de proximitate atât de nou formată ar fi
| clusterele | (A, B) | C | D | E |
| (A, B) | 0 | 18 | 10 | 25 |
| C | 18 | 0 | 8 | 7 |
| D | 10 | 8 | 0 | 15 |
| E | 25 | 7 | 15 | 0 |
În iterația 2, 7 este distanța minimă, prin urmare, unim C și E formând un nou cluster (C, E), repetăm procesul urmat în iterația 1 până terminăm cu un singur cluster, aici ne oprim la iterația 4.
Întregul proces este prezentat în figura de mai jos:
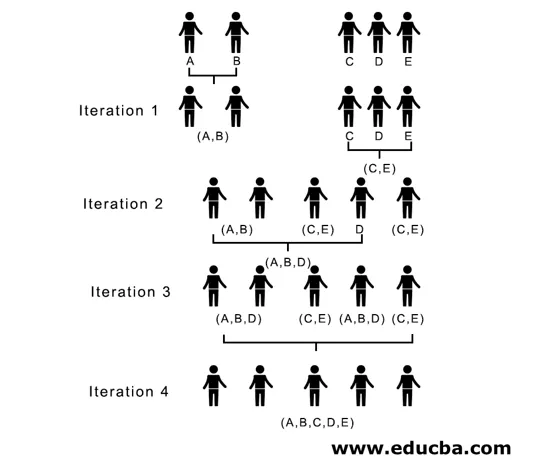
(A, B, D) și (D, E) sunt cele 2 grupuri formate la iterația 3, la ultima iterație putem vedea că am rămas cu un singur cluster.
2. Clustering diviziv
Pentru început, considerăm toate punctele ca un singur cluster și le separăm la distanța cea mai îndepărtată până când terminăm cu puncte individuale ca grupuri individuale (nu neapărat ne putem opri la mijloc, depinde de numărul minim de elemente pe care le dorim în fiecare cluster) la fiecare pas. Este exact opusul grupărilor aglomerative și este o abordare de sus în jos. Clusteringul diviziv este o modalitate în care repetitivul k înseamnă clustering.
Alegerea dintre aglomerarea și divulgarea divizivă depinde din nou de aplicație, însă câteva puncte de luat în considerare sunt:
- Divizivul este mai complex decât grupările aglomerative.
- Clusterizarea divizivă este mai eficientă dacă nu generăm o ierarhie completă până la punctele de date individuale.
- Gruparea aglomerativă ia o decizie luând în considerare modelele locale, fără a ține cont de tiparele globale inițial care nu pot fi inversate.
Vizualizarea clusterării ierarhice
O metodă super utilă pentru vizualizarea grupării ierarhice care ajută în afaceri este Dendograma. Dendogramele sunt structuri asemănătoare arborelor, care înregistrează secvența de fuziuni și diviziuni în care linia verticală reprezintă distanța dintre clustere, distanța dintre liniile verticale și distanța dintre clustere este direct proporțională, adică cu cât distanța este mai mare decât cea mai mare.
Putem folosi dendograma pentru a decide numărul de clustere, doar să desenăm o linie care se intersectează cu o linie verticală cea mai lungă pe dendogramă, un număr de linii verticale intersectate va fi numărul de clustere care trebuie luate în considerare.
Mai jos este exemplul Dendogramă.
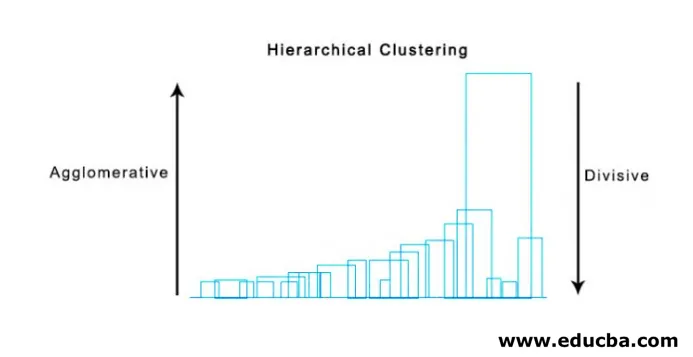
Există pachete de piton destul de simple și directe și funcțiile sale sunt de a efectua agregarea ierarhică a grupurilor și dendogramelor.
- Ierarhia de la scipy.
- Cluster.hierarchy.dendogram pentru vizualizare.
Scenarii comune în care se folosește clusteringul ierarhic
- Segmentarea clientului la comercializarea produselor sau serviciilor.
- Planificare urbană pentru identificarea locurilor pentru construirea structurilor / serviciilor / clădirii.
- Analiza rețelelor sociale, de exemplu, identificați toți fanii MS Dhoni pentru a-și face reclama biopicului său.
Avantajele grupării ierarhice
Avantajele sunt prezentate mai jos:
- În cazul clusterării parțiale precum mijloacele k, numărul de clustere ar trebui să fie cunoscut înainte de clustering, ceea ce nu este posibil în aplicații practice, în timp ce în grupări ierarhice nu este necesară cunoașterea prealabilă a numărului de clustere.
- Clusterizarea ierarhică produce o ierarhie, adică o structură mai informativă decât setul nestructurat al grupurilor plate returnate prin clustering parțial.
- Clusterizarea ierarhică este ușor de implementat.
- Prezintă rezultate în majoritatea scenariilor.
Concluzie
Tipul de clustering face cea mai mare diferență atunci când sunt prezentate datele, clustering-ul ierarhic fiind mai informativ și ușor de analizat este mai preferat decât clusteringul parțial. Și este adesea asociat cu hărțile de căldură. Să nu uităm atributele alese pentru a calcula similitudinea sau disimilaritatea influențează predominant atât clustere cât și ierarhie.
Articole recomandate
Acesta este un ghid pentru clusteringul ierarhic. Aici vom discuta despre introducerea, avantajele clusterării ierarhice și a scenariilor comune în care se folosește clusterul ierarhic. Puteți parcurge și alte articole sugerate pentru a afla mai multe -
- Algoritmul de clustering
- Gruparea în învățarea mașinilor
- Gruparea Ierarhică în R
- Metode de clustering
- Cum să elimini Ierarhia din Tableau?