Exemplu de dobândă compusă - Exemple practice cu formula

Exemplu de introducere în interesul compus

Există numeroase exemple de interes compus. Următorul exemplu de interes compus diferit oferă o înțelegere a celui mai frecvent tip de situații în care se calculează interesul compus și cum se poate calcula același lucru. Deoarece există mai multe domenii și situații în care poate fi calculată interesul compus, nu este posibil să oferim toate tipurile de exemple. Așadar, câteva dintre exemple de interes compus sunt prezentate mai jos care arată diferitele situații

Exemple de interes compus (cu șablonul Excel)

Să luăm un exemplu pentru a înțelege calculul dobânzii compuse într-o manieră mai bună.

Puteți descărca acest șablon Excel Exemplu de interes compus aici - Exemplu Excel Exemplu de interes compus Și mai jos sunt exemple de interes compus:

Exemplu de dobândă compusă -1

Harry vrea să înceapă economiile din banii câștigați de el. Apoi decide să depună suma inițială de 10.000 USD în contul de economii cu dobândă mare. Rata dobânzii, în acest caz, va fi de 15% pe an, combinată anual. În prezent, vârsta harry este de 40 de ani și intenționează să ia pensie la vârsta de 60 de ani. Acest lucru înseamnă că Harry are orizontul de timp de 40 de ani peste el poate acumula interesul. Calculați suma de bani pe care Harry o va primi la vârsta de 60 de ani. De asemenea, pregătește tabelul pentru a afișa interesul anual și valoarea contului.

Dat,

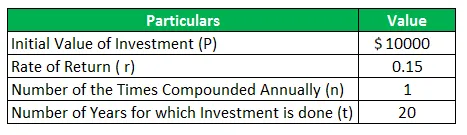
Soluţie:

Folosind informațiile furnizate, calculul dobânzii compuse și a sumei de primit la vârsta de 60 de ani este următorul:

Calculul valorii viitoare a investițiilor folosind formula dobânzii compuse este după cum urmează:

A = P (1 + r / n) ^nt

A = 10.000 $ (1 + 0.15 / 1) ^{1 * 20}
A = 10.000 $ (1 + 0, 15) ²⁰
A = 10.000 $ (1, 15) ²⁰
A = 10.000 USD * 16.367
A = 163.665, 37 USD

Tabel pentru a afișa interesul anual și valoarea contului

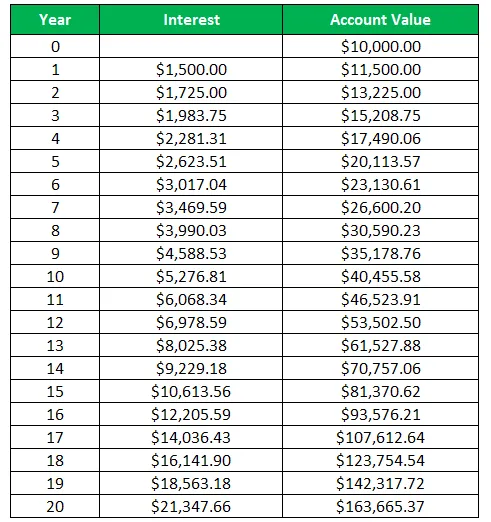
Aici dobânda este calculată ca:

Dobândă = Suma inițială a investiției * Rata dobânzii (r)
Dobândă = 10000 * 15%
Dobândă = 1500 $

În mod similar pentru toți anii.

iar valoarea contului se calculează ca:

Valoarea contului = Suma inițială a investiției + dobândă
Valoarea contului = 10000 + 1500
Valoarea contului = 11500 $

În mod similar pentru toți anii.

În prezentul exemplu, putem vedea că valoarea contului investiției realizate inițial de 10.000 USD devine 163.665, 37 USD la sfârșitul perioadei de 20 de ani. Acest lucru evidențiază puterea compunerii, întrucât, cu ajutorul dobânzilor compuse, și-a înmulțit banii în mai multe ori, fără a gestiona investiția în mod activ. Aici Harry a putut să câștige și interesul asupra dobânzii câștigate anterior.

Exemplu de dobândă compus -2

Sam realizează o investiție inițială de 10.000 USD pentru o perioadă de 5 ani. El dorește să cunoască valoarea investiției pe care o va obține după cei 5 ani, dacă investiția câștigă o rentabilitate de 6% pe an, combinată săptămânal.

Dat,

Folosind informațiile furnizate, calculul dobânzii compuse și a sumei de primit după perioada de 5 ani este următoarea:

Soluţie:

Calculul valorii viitoare a unei investiții folosind formula dobânzii compuse este următorul:

A = P (1 + r / n) ^nt

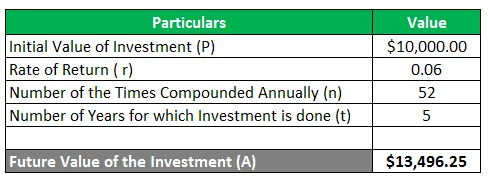
A = 10.000 $ (1 + 0.6 / 52) ^{52 * 5}

A = 10.000 $ (1 + 0.00115) ²⁶⁰

A = 10.000 $ (1.00115) ²⁶⁰

A = 10.000 USD * 1.3496

A = 13.496, 25 USD

În prezentul exemplu, putem observa că valoarea contului investiției realizate inițial de 10.000 USD devine 13.496, 25 USD la sfârșitul perioadei de 5 ani, când compunerea se face săptămânal. Compunerea crește valoarea investiției la sfârșitul perioadei, pe măsură ce dobânzile sunt obținute și asupra dobânzii câștigate anterior. Aici, compunerea se face de 52 de ori, deoarece sunt 52 de săptămâni într-un an.

Concluzie - Exemplu de dobândă compusă

Dobânda compusă dă mai multă dobândă în comparație cu dobânda simplă, deoarece este derivată prin perceperea dobânzii la principalul restant, inclusiv dobânda spre deosebire de dobânda simplă, în cazul în care dobânda este percepută pe suma principală inițială și nu se percepe nicio dobândă peste dobândă. Puterea de compunere ajută la creșterea investiției cu mai multă viteză având caracteristicile funcției exponențiale. Este rezultatul faptului că, în ciuda plății investiției, sunt reinvestite pentru a crește mai repede. Acest lucru este foarte des utilizat în practicile normale ale afacerii, fie că este cazul împrumutului sau depozitului. Mai mult decât atât, cât de des se face compunerea va fi și factorul decisiv pentru creștere. Să presupunem că, dacă la o anumită rată, frecvența de compunere este pe lună, rata anuală a acesteia va fi mai mare decât cea a frecvenței de compunere semestrială sau anuală.

Articole recomandate

Acesta a fost un ghid pentru Exemplul de interese compuse. Aici vom discuta despre cum să calculăm interesul compus folosind formula sa împreună cu exemple practice. De asemenea, puteți arunca o privire la următoarele articole pentru a afla mai multe -