
Coeficientul formulei de variație (cuprins)
- Formulă
- Exemple
Care este coeficientul formulei de variație?
În statistici, coeficientul de variație denumit și CV este un instrument care ne ajută să determinăm modul în care punctele de date dintr-un set de date sunt distribuite în jurul mediei. Practic, toate punctele de date sunt reprezentate mai întâi și apoi coeficientul de variație este utilizat pentru a măsura dispersia punctelor respective unul de la altul și media. Deci ne ajută să înțelegem datele și, de asemenea, să vedem modelul pe care îl formează. Se calculează ca un raport dintre abaterea standard a setului de date la valoarea medie. Coeficientul de variație mai mare înseamnă că există un nivel mai mare de dispersie a datelor în jurul mediei. În mod similar, cu cât scade valoarea coeficientului de variație, cu atât este mai mică dispersia și mai precise vor fi rezultatele. Chiar dacă media a două serii de date este considerabil diferită, coeficientul de variație este foarte util pentru a compara gradul de variație de la o serie de date la alta.
Formula pentru coeficientul de variație este dată de:
Coefficient of Variation = Standard Deviation / Mean
Pași pentru calcularea coeficientului de variație:
Pasul 1: Calculați media setului de date. Media este media tuturor valorilor și poate fi calculată luând suma tuturor valorilor și apoi împărțind-o la un număr de puncte de date.
Pasul 2: Apoi calculați abaterea standard a setului de date. Acesta este un proces care consumă puțin timp. Abaterea standardelor poate fi calculată astfel: √ (Σ (X i - X m ) 2 / (n - 1)) . X i este punctul de date și X m este media setului de date. Alternativ, putem găsi, de asemenea, abaterea standard în excel, folosind funcția STDEV.S ().
Pasul 3: Împărțiți abaterea standard la medie pentru a obține coeficientul de variație.
Exemple de formulă de coeficient de variație (cu șablonul Excel)
Să luăm un exemplu pentru a înțelege calculul coeficientului de variație într-o manieră mai bună.
Puteți descărca aici șablonul Coeficient de variație cu formula de variație - Coeficient de șablon cu formula de variațieCoeficientul formulei de variație - Exemplul # 1
Să zicem că avem două seturi de date A & B și fiecare conține 20 de puncte aleatorii. Calculați coeficientul de variație pentru setul de date X & Y.
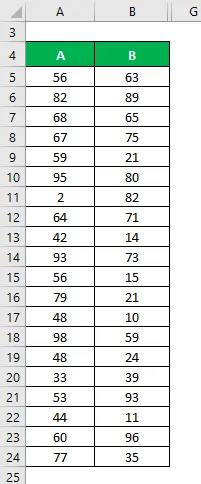
Soluţie:
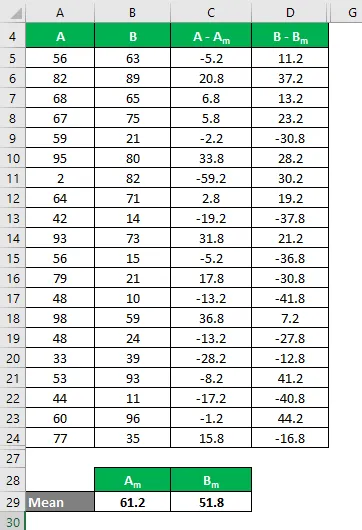
Media este calculată ca:
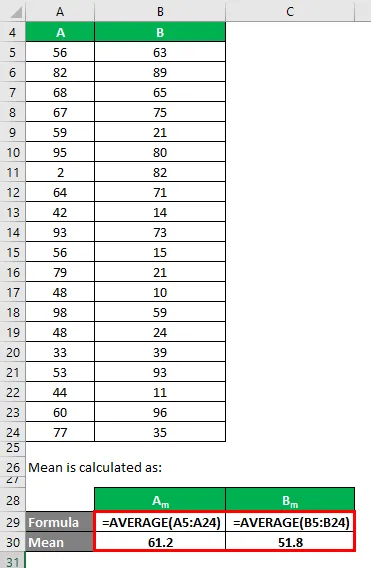
- Media setului de date A = 61.2
- Media setului de date B = 51, 8
Acum, trebuie să calculăm diferența dintre punctele de date și valoarea medie.
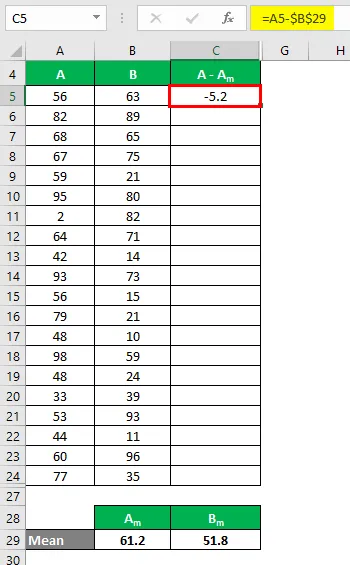
În mod similar, calculați pentru toate valorile setului de date A.
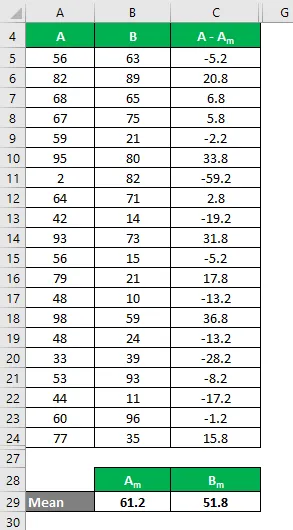
În mod similar, calculați pentru toate valorile setului de date B.
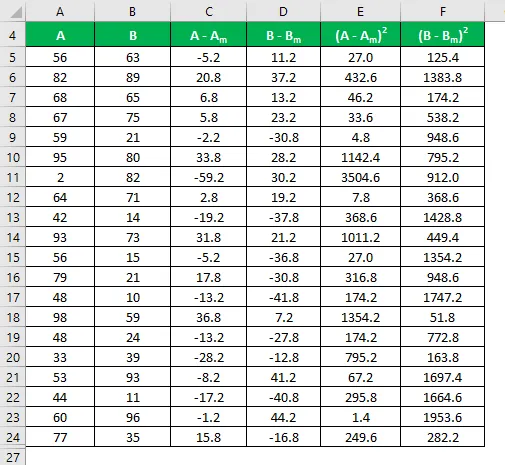
Calculați pătratul diferenței pentru ambele seturi de date A și B.
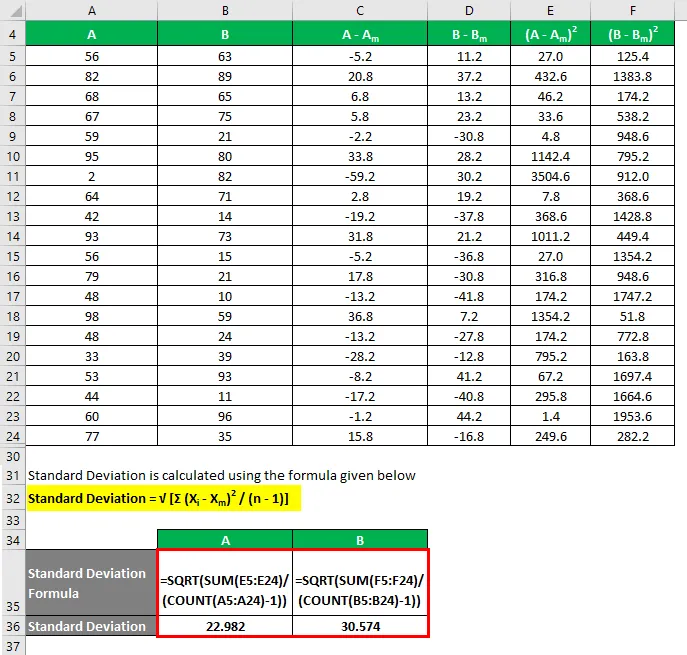
Abaterea standard este calculată folosind formula prezentată mai jos
Abatere standard = √ (Σ (X i - X m ) 2 / (n - 1))
Coeficientul de variație este calculat folosind formula dată mai jos
Coeficient de variație = Abatere standard / medie
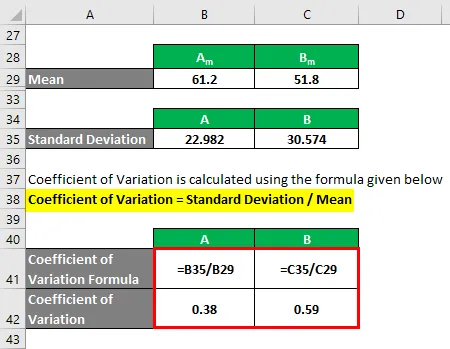
- Coeficientul variației A = 22.982 / 61, 2 = 0, 38
- Coeficientul variației B = 30.574 / 51, 8 = 0, 59
Deci, dacă vedeți aici, B are un coeficient de variație mai mare decât A, ceea ce înseamnă că punctele de date ale B sunt mai dispersate decât A.
Coeficientul formulei de variație - Exemplul # 2
Să spunem că sunteți un investitor foarte riscant și căutați să investiți bani pe piața bursieră. Deoarece pofta de risc este scăzută, doriți să investiți în stocuri sigure care au o abatere standard mai mică și coeficient de variație. Ați selectat 3 acțiuni pe baza informațiilor lor fundamentale și tehnice și doriți să alegeți 2 stocuri. De asemenea, ați colectat informații despre profiturile lor istorice din ultimii 15 ani.
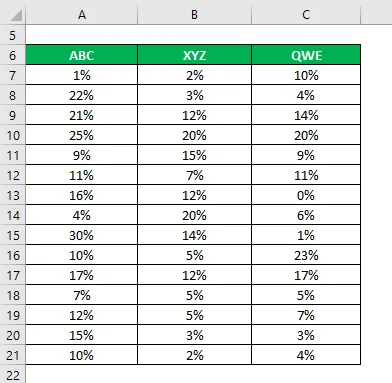
Soluţie:
Media este calculată ca:
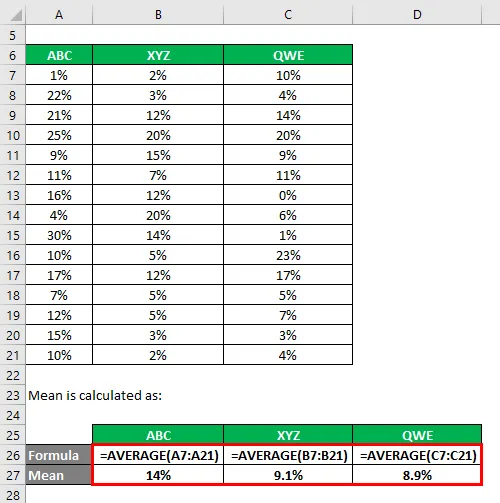
Abaterea standard este calculată folosind formula excel
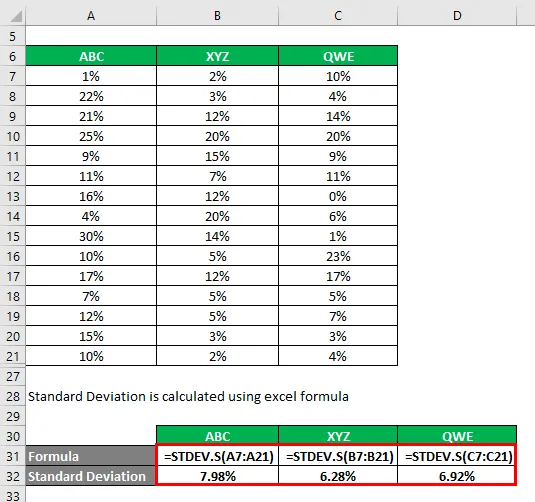
Coeficientul de variație este calculat folosind formula dată mai jos
Coeficient de variație = Abatere standard / medie
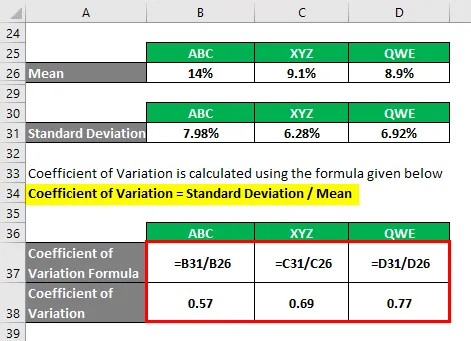
- Coeficientul de variație ABC = 7, 98% / 14% = 0, 57
- Coeficientul de variație XYZ = 6, 28% / 9, 1% = 0, 69
- Coeficientul de variație QWE = 6, 92% / 8, 9% = 0, 77
Pe baza informațiilor, veți alege stocul ABC și XYZ pentru a investi, deoarece acestea au cel mai mic coeficient de variație.
Explicaţie
Deoarece coeficientul de variație este o măsură a riscului, acesta ajută la măsurarea volatilității prețurilor stocurilor și a altor instrumente financiare. De asemenea, ajută investitorii și analiștii să compare riscurile asociate cu diferite investiții potențiale.
Coeficientul de variație este similar cu abaterea standard, dar o abatere standard a două variabile nu poate fi comparată în mod util. Dar folosirea abaterii standard și a mediei face ca comparația relativă să fie mai semnificativă. Există, de asemenea, o limitare a coeficientului de variație. Să presupunem că media unui set de date este zero. În acest caz, acest instrument va deveni ineficient. Nu numai acest lucru, dacă avem un set de date care are multe valori pozitive și negative, coeficientul de variație devine foarte problematic. Deci este mai util doar seturile de date care au același semn plus-minus.
Relevanța și utilizările formulei de coeficient de variație
Coeficientul de variație are relevanță în multe alte domenii, altele decât statisticile. De exemplu, în domeniul finanțelor, coeficientul de variație este o măsură a riscului. Este similar cu abaterea standard, deoarece aceasta este folosită și ca măsură a riscului, dar diferența este că coeficientul de variație este un indicator mai bun al riscului relativ. De exemplu, să spunem că randamentul preconizat al lui A este de 15% și randamentul preconizat al lui B de 10% și A are o abatere standard de 10%, în timp ce B are o abatere standard de 5%. Pentru a alege o investiție mai bună, se poate utiliza coeficientul de variație. Deci coeficientul de variație al lui A este 10/15 = 0, 666 și coeficientul de variație al lui B este 5/10 = 0, 5. Deci B este o investiție mai bună decât A.
Articole recomandate
Acesta a fost un ghid pentru formula coeficientului de variație. Aici vom discuta despre cum să calculăm coeficientul de variație folosind formula împreună cu exemple practice și șablon Excel descărcabil. De asemenea, puteți consulta următoarele articole pentru a afla mai multe -
- Ce este Formula R Squared ajustată?
- Exemple de formulă de coeficient de determinare
- Cum se calculează coeficientul de corelație folosind formula?
- Formula de convergență cu șablon Excel