
Introducere în Merge Sort în JavaScript
Algoritmii de sortare sunt foarte importanți în informatică. Rezultatul sortării este de a aranja elementele unei liste la o anumită ordine (ascendentă sau descendentă). Merge Sortare în JavaScript este unul dintre cei mai eficienți algoritmi de sortare disponibili, întrucât se bazează pe conceptul de divizare și cucerire. După cum sugerează și numele, mai întâi împărțiți problema mai mare în probleme mici decât rezolvați problemele mai mici pentru a rezolva problema mai mare. Conceptual, sortarea Merge este o combinație de doi algoritmi de bază numiți MERGE și MERGE_SORT.
care funcționează astfel:
- Împărțiți lista nesortată în n număr de subliste cu un singur articol (n este numărul total de elemente din lista nesortată).
- Fuzionați repetat subliste în subliste sortate până când nu există decât o listă sortată.
Implementarea sortării Merge în JavaScript
Algoritmul MERGE urmează procedura combinării a două liste sortate într-o listă sortată.
Exemplu: Să presupunem că există două liste, adică Lista 1 (1, 5, 3) și Lista 2 (7, 2, 9).
1. Sortează mai întâi ambele liste.
Acum, vom vedea și vom aplica tehnica E pe ea.
2. Apoi, vom crea o nouă listă cu dimensiunea x + y unde x este numărul de elemente din Lista 1 și y este numărul de elemente din Lista 2.

În cazul nostru x = 3 și y = 3, deci x + y = 6.
3. Acum, avem doi indicatori.
Un prim indicator care indică prima poziție a listei 1 și un al doilea indicator îndreptat către prima poziție a listei 2.

4. Apoi vom compara valoarea ambelor indicatoare. Indicatorul cu valoare mai mică, copiați elementul în Lista 3 și mutați indicatorul la dreapta listei cu o valoare mai mică și lista rezultată (adică Lista 1 și Lista 3)

5. În mod similar, efectuați iar și iar pasul 4.

Parcurgerea ulterioară …
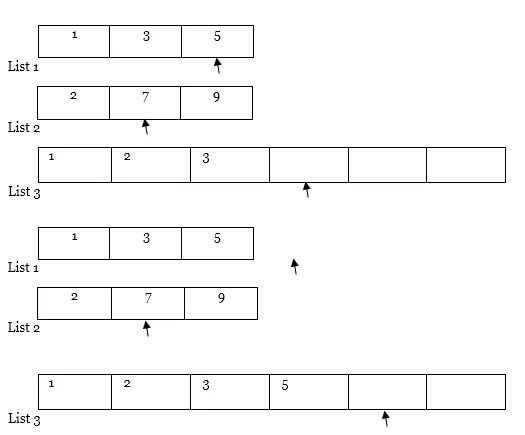
Notă : Dacă una dintre liste (adică lista 1 sau lista 2) este parcursă complet ca în caz, atunci copiați întregul conținut al altei liste de la pointer la lista de rezultate (adică lista 3) după cum urmează.

Pseudo cod
Function merge (sublist1, sublist2) (
Create var for result list
While sublist1 length > 0 and sublist2 length > 0
If sublist1(0) < sublist2(0) Copy the sublist1 pointer value to result list and Shift pointer of sublist1 to right
else
Copy the sublist2 pointer value to result list and Shift pointer of sublist2 to right
Return concat sublist1 or sublist2 (depending if node1 is empty or not)
Algoritmul MERGE_SORT împarte lista nesortată dată la dimensiunea minimă și apoi apelează algoritmul MERGE pentru a combina lista în noua listă sortată.
Pseudo cod
function mergeSort(list) (
If list length < 2
Return list
Create var for middle index of list
Create var for left index of list
Create var for right index of list
Recursively call mergeSort function
)
Exemplu
Aici urmăm punerea în aplicare de top-down Merge Sort. Începe de sus și continuă spre jos, cu fiecare rând recursiv punând aceeași întrebare „Ce trebuie făcut pentru a sorta lista?”, Iar răspunsul este „Împărțiți lista în două, efectuați un apel recursiv și îmbinați rezultate“.
Cod în Javascript
// Split the list into halves and merge them recursively
function mergeSort (list) (
if (list.length < 2) (
return list;// return once we hit a list with a single element
)
var mid = Math.floor(list.length / 2);
var left = mergeSort(list.slice(0, mid));
var right = mergeSort(list.slice(mid));
return merge(left, right);
)
// compare the lists element by element and return the concatenated resultList
function merge (sublist1, sublist2) (
var resultList = ();
while (sublist1.length > 0 && sublist2.length > 0)
resultList.push(sublist1(0) < sublist2(0)? sublist1.shift() : sublist2.shift());
return resultList.concat(sublist1.length? sublist1 : sublist2);
)
const list = (6, 5, 3, 1, 8, 7, 2, 4, 2, 5, 1, 2, 3) console.log(mergeSort(list)) //( 1, 1, 2, 2, 2, 3, 3, 4, 5, 5, 6, 7, 8 )
Funcția principală a sortării de îmbinare va împărți lista dată în liste mai mici în fiecare iterație a apelului recursiv. Nu uitați că recursiunea necesită condiția de bază pentru a evita recursiunea infinită. În cazul nostru, avem:
if (list.length < 2) (
return list;// return once we hit a list with a single element
)
După ce am stabilit condiția de bază pentru recurs, atunci vom identifica indexul de mijloc pentru a împărți lista dată în sub-lista din stânga și dreapta așa cum puteți vedea mai sus în diagrama de exemplu. Apoi, trebuie să îmbinăm sub-lista stângă și sub-lista dreaptă pe care o vom arăta acum, În funcția de îmbinare de mai sus, trebuie să ne asigurăm că sortăm toate elementele din sublista din stânga și sub-lista dreaptă. listă. Modul în care vom face acest lucru este folosind o buclă de timp. În bucla while, vom compara elementul din sublista din stânga și elementul din sub-lista din dreapta unul câte unul. Îl putem împinge pe cel mai mic dintre cei doi în lista de rezultate și putem muta în mod corespunzător cursorul sub-listei din stânga și al sub-listei drepte. În cele din urmă, trebuie să concatenăm lista de rezultate. Este foarte important! Dacă nu facem acest ultim pas aici, vom avea o listă incompletă de elemente la sfârșit, deoarece starea de buclă în timp ce va eșua odată ce oricare dintre cei doi indicatori ajunge la final.
ieşire:

Proprietăți de Merge Sort
- Sortul de îmbinare este stabil, deoarece același element dintr-un tablou își menține pozițiile inițiale unul față de celălalt.
- Sortarea Merge nu este „la loc”, deoarece în timpul contopirii creează o copie a întregii liste care este sortată. Datorită acestui fapt, complexitatea spațială (O (n)) a acestui algoritm este de fapt mai mare decât alții, și nu trebuie utilizată în probleme complexe unde spațiul este premium.
- Complexitatea de timp generală a sortării Merge este O (nLogn). Este mai eficient, deoarece este și în cel mai rău caz, timpul de rulare este O (nlogn).
Concluzie
Complexitatea timpului cel mai bun, cel mai rău și cel mediu este același, ceea ce îl face un algoritm mai eficient. Funcționează mai repede decât alte tehnici de sortare. Sortare combinată poate fi aplicată fișierelor de orice dimensiune. Este foarte paralizabil datorită utilizării metodei de împărțire și de cucerire. Pentru a dezvolta elemente de bază puternice în informatică, vi se recomandă să înțelegeți în detaliu diferiți algoritmi de sortare.
Articol recomandat
Acesta a fost un ghid pentru Merge Sort în JavaScript. Aici discutăm Introducere în Merge Sort în JavaScript și Implementare împreună cu Proprietăți. Puteți parcurge și alte articole sugerate pentru a afla mai multe -
- Funcții matematice JavaScript
- Introducere în JavaScript
- Cele mai bune cadre JavaScript
- Instrumente JavaScript
- Top 6 Sortarea algoritmului în JavaScript