
Introducere în algoritmul DFS
DFS este cunoscut sub numele de algoritmul de căutare în adâncime, care oferă pașii pentru a traversa fiecare nod al unui grafic fără a repeta niciun nod. Acest algoritm este același ca Depth First Traversal pentru un arbore, dar diferă în menținerea unui boolean pentru a verifica dacă nodul a fost deja vizitat sau nu. Acest lucru este important pentru traversarea graficului, deoarece ciclurile există și în grafic. În acest algoritm se păstrează o stivă pentru a stoca nodurile suspendate în timpul traversării. Este numit așa pentru că mai întâi călătorim la adâncimea fiecărui nod adiacent și apoi continuăm să parcurgem un alt nod adiacent.
Explicați algoritmul DFS
Acest algoritm este contrar algoritmului BFS unde sunt vizitate toate nodurile adiacente urmate de vecini către nodurile adiacente. Începe să exploreze graficul dintr-un singur nod și explorează profunzimea sa înainte de backtracking. Două lucruri sunt luate în considerare în acest algoritm:
- Vizitarea unui vertex: selectarea unui vertex sau a unui nod al graficului de trasat.
- Explorarea unui vertex: Traversarea tuturor nodurilor adiacente acelui vertex.
Cod Pseudo pentru adâncime Prima căutare :
proc DFS_implement(G, v):
let St be a stack
St.push(v)
while St has elements
v = St.pop()
if v is not labeled as visited:
label v as visited
for all edge v to w in G.adjacentEdges(v) do
St.push(w)
Linear Traversal există, de asemenea, pentru DFS care poate fi implementat în 3 moduri:
- Pre-comanda
- Pentru a
- postordine
Postorder invers este un mod foarte util de a traversa și utilizat în sortarea topologică, precum și diverse analize. De asemenea, se păstrează o stivă pentru a stoca nodurile a căror explorare este încă în curs.
Travers grafic în DFS
În DFS, etapele de mai jos sunt urmate pentru a traversa graficul. De exemplu, un grafic dat, să începem traversarea de la 1:
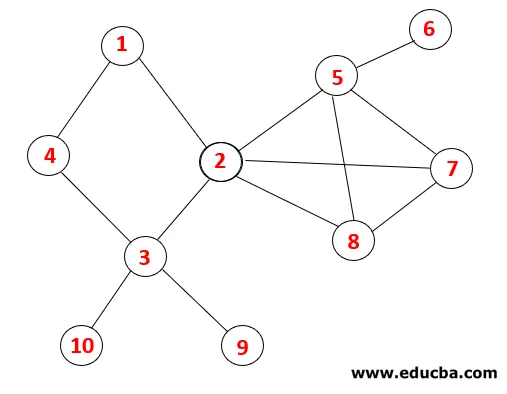
| Grămadă | Secvență traversală | Spanning Tree |
| 1 |  |
|
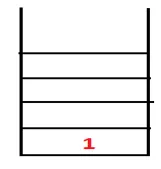 | 1, 4 |  |
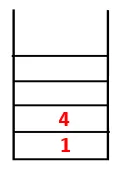 | 1, 4, 3 |  |
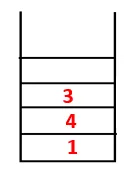 | 1, 4, 3, 10 | 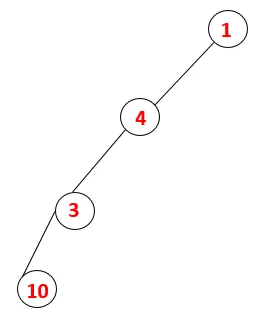 |
 | 1, 4, 3, 10, 9 | 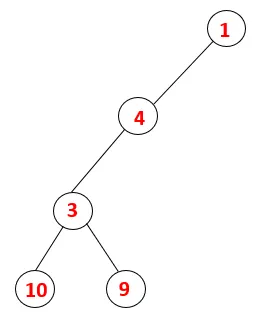 |
 | 1, 4, 3, 10, 9, 2 | 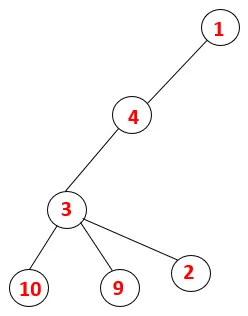 |
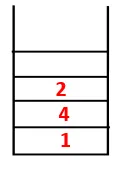 | 1, 4, 3, 10, 9, 2, 8 |  |
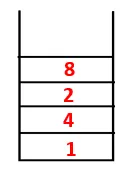 | 1, 4, 3, 10, 9, 2, 8, 7 | 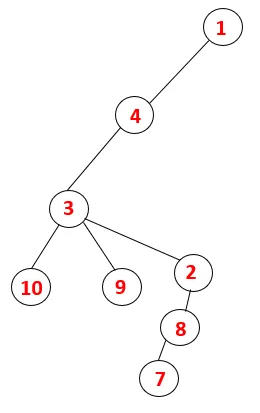 |
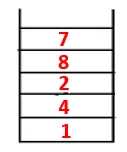 | 1, 4, 3, 10, 9, 2, 8, 7, 5 |  |
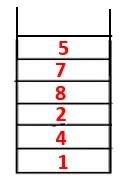 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 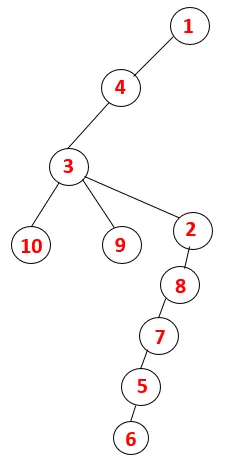 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 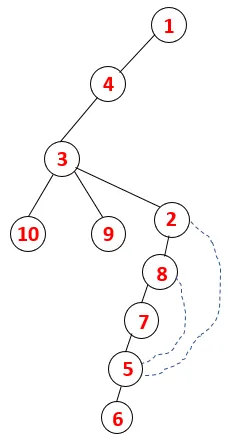 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
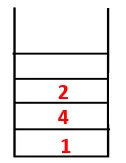 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 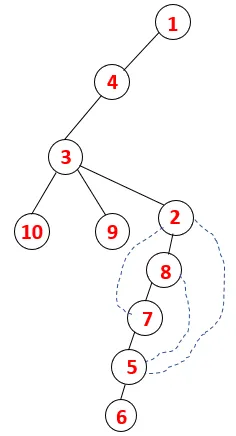 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 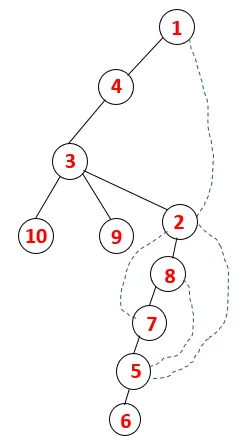 |
Explicație pentru algoritmul DFS
Mai jos sunt pașii pentru algoritmul DFS cu avantaje și dezavantaje:
Pasul 1: Nodul 1 este vizitat și adăugat la secvență, precum și arborele de întindere.
Pasul 2: Se explorează nodurile adiacente de la 1, care este 4, astfel încât 1 este împins la stivă și 4 este împins în secvență, precum și în arborele de acoperire.
Pasul 3: Unul dintre nodurile adiacente ale 4 este explorat și astfel 4 este împins către stivă, iar 3 intră în secvența și arborele de întindere.
Pasul 4: Nodurile adiacente din 3 sunt explorate prin împingerea acesteia pe stivă și 10 intră în secvență. Deoarece nu există un nod adiacent la 10, astfel 3 sunt scoase din stivă.
Pasul 5: Un alt nod adiacent de 3 este explorat și 3 este împins pe stivă și 9 este vizitat. Niciun nod adiacent de la 9 astfel 3 este declanșat și ultimul nod adiacent de 3 adică 2 este vizitat.
Un proces similar este urmat pentru toate nodurile până când stiva devine goală, ceea ce indică starea de oprire a algoritmului de traversare. - -> linii punctate în arborele de întindere se referă la marginile din spate prezente în grafic.
În acest fel, toate nodurile din grafic sunt transversale, fără a repeta niciunul dintre noduri.
Avantaje și dezavantaje
- Avantaje: Această cerință de memorie pentru acest algoritm este foarte mică. Complexitate de spațiu și timp mai mică decât BFS.
- Dezavantaje: Soluția nu este garantată Aplicații. Sortare topologică. Găsirea Punților de grafic.
Exemplu pentru implementarea algoritmului DFS
Mai jos este exemplul de implementare a algoritmului DFS:
Cod:
import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)
ieşire:
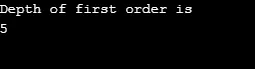
Explicație la programul de mai sus: Am realizat un grafic având 5 vârfuri (0, 1, 2, 3, 4) și am folosit tabloul vizitat pentru a urmări toate vârfurile vizitate. Apoi pentru fiecare nod ale cărui noduri adiacente există același algoritm se repetă până când toate nodurile sunt vizitate. Apoi, algoritmul revine la apelul la vertex și îl deschide din stivă.
Concluzie
Cerința de memorie a acestui grafic este mai mică comparativ cu BFS, deoarece este necesară menținerea unei singure stive. Ca urmare, este generat un arbore de secvență și traversare DFS, dar nu este constant. Secvența de traversare multiplă este posibilă în funcție de vertexul de început și de vertexul de explorare ales.
Articole recomandate
Acesta este un ghid pentru algoritmul DFS. Aici discutăm explicația pas cu pas, traversăm graficul într-un format de tabel cu avantaje și dezavantaje. Puteți parcurge și alte articole conexe pentru a afla mai multe -
- Ce este HDFS?
- Algoritmi de învățare profundă
- Comenzi HDFS
- Algoritmul SHA