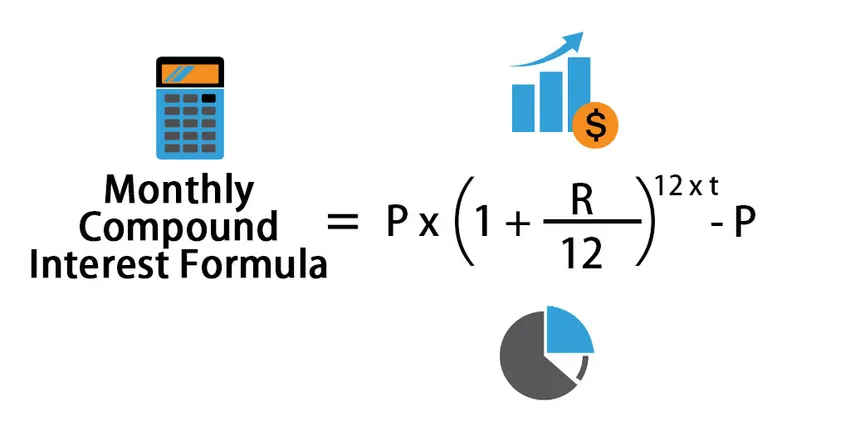
Formula lunară de dobândă compusă (cuprins)
- Formulă
- Exemple
- Calculator
Care este formula lunară de dobândă compusă?
Atunci când o anumită sumă de bani este împrumutată pentru o anumită durată, iar o sumă suplimentară trebuie plătită împreună cu suma împrumutată. Apoi suma suplimentară pe care o plătim la rata fixă se numește dobândă. Interesul compus este interesul total care include interesul inițial și interesul noului principal, care este evoluat prin adăugarea principalului inițial la interesul cuvenit. Pentru calculul lunar compus pentru calcul, dobânzile care se acumulează toată luna în tot anul.
Formula de dobândă lunară compusă poate fi calculată ca:
Monthly Compound Interest Formula = P * (1 + (R /12)) 12*t – P
Unde,
- P = suma principală
- R = rata
- t = Timp
Exemple de formulă lunară de dobândă compusă (cu șablonul Excel)
Să luăm un exemplu pentru a înțelege calculul dobânzii compuse lunare într-o manieră mai bună.
Puteți descărca acest șablon Formula de dobândă compusă lunară aici - Modelul de formare a dobânzii compuse lunareFormula de dobândă compusă lunară - Exemplul # 1
Un împrumutat a împrumutat o sumă de Rs 10.000 la o rată de 8%. Calculați rata dobânzii lunare compuse pentru 2 ani?
Soluţie:
Dobânda lunară compusă se calculează folosind formula de mai jos
Dobânda lunară compusă = P * (1 + (R / 12)) 12 * t - P
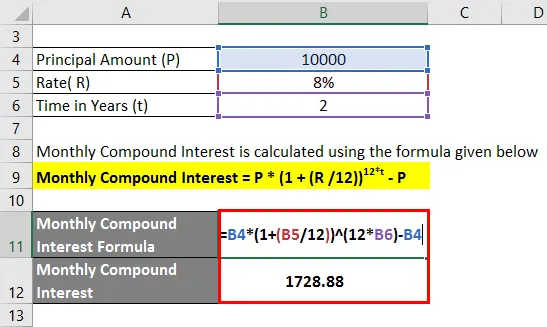
- Dobânda lunară compusă = 10.000 (1 + (8/12)) 2 * 12 - 10.000
- Dobânda lunară compusă = 1.728, 88
Interesul compus lunar timp de 2 ani este de Rs 1, 728.88
Formula dobânzii compuse lunare - Exemplul # 2
O sumă de bani este investită cu o rată de 10% este de 20.000 Rs. Care va fi dobânda combinată lunară pentru cei 10 ani?

Soluţie:
Dobânda lunară compusă se calculează folosind formula de mai jos
Dobânda lunară compusă = P * (1 + (R / 12)) 12 * t - P
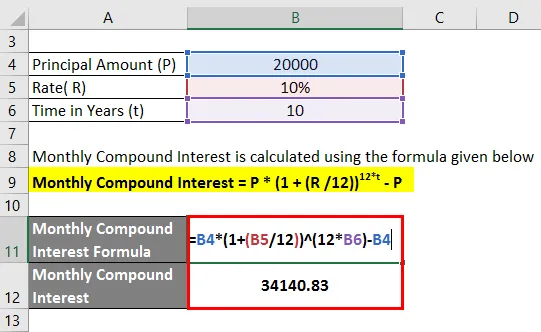
- Dobânda lunară compusă = 20.000 (1 + 10/12)) 10 * 12 - 20.000
- Dobânda lunară compusă = 34.140, 83
Dobânda lunară compusă pentru 10 ani este Rs 34.140, 83
Formula dobânzii compuse lunare - Exemplul # 3
Doamna Jefferson a cumpărat un statut antic pentru 500 de dolari. Cinci ani mai târziu, a vândut acest statut pentru 800 de dolari. Ea a considerat-o ca o parte a investiției. Calculați rata anuală pe care a obținut-o?
Soluţie:
Dacă avem în vedere o investiție de 500 de dolari și obținem 800 de dolari în viitorul interval de timp după t = 10 ani. Ne asumăm o rată anuală m = 1 și o implementăm în formulă.
A = P (1 + r / m) mt
- 800 = 500 (1+ r / 1) 1 * 10
- 800 = 500 (1 + r) 10
Acum, rezolvăm rata (r) în următorii pași.
- 800 = 500 (1 + r) 10
- 8/5 = (1 + r) 10
Acum, luăm puterea de (1/10) în partea stângă a ecuației și ștergem din partea dreaptă.
- (8/5) 1/10) = 1 + r
Calculați valoarea din stânga și rezolvați pentru r.
- 1.0481 = 1 + r
- 1.0481 - 1 = r
- 0, 0481 = r
Cu toate acestea, doamna Jefferson a obținut rata dobânzii anuale de 4, 81%, ceea ce nu este o rată de rentabilitate proastă.
Explicaţie
Dobânda compusă este produsul sumei principale inițiale cu unu plus rata dobânzii anuale ridicată la numărul de perioade compuse minus una. Deci valoarea inițială a împrumutului este scăzută din valoarea rezultată.
Interesul compus poate fi calculat cum ar fi:
Formula dobânzii compuse = (P (1 + i) n ) - P
Formula dobânzii compuse = (P (1 + i) n - 1)
Unde:
- P = suma principală
- i = Rata anuală a dobânzii în termeni de procent
- n = perioade compuse
Există un anumit set de proceduri prin care putem calcula Dobânda lunară compusă.
Pasul 1: Trebuie să calculăm cantitatea de dobândă obținută folosind dobânda de compunere lunară. Formula poate fi calculată astfel:
- A = (P (1 + i) n - 1) - P
Pasul 2: dacă presupunem că rata dobânzii este de 5% pe an. În primul rând, trebuie să exprimăm valoarea ratei dobânzii în numărul zecimal echivalent. Acest lucru se poate face în felul următor.
- 5% = 5/100 = 0, 05
Pasul 3: După cum știm că dobânda se mărește lunar, deci putem lua n = 12. Cu toate acestea, perioada de timp este specificată în acest caz, am considera că împrumutul este luat pentru o perioadă de un an. Acum, avem toate variabilele disponibile la noi pe care le putem substitui direct în formulă și obținem rezultatul din aceasta.
- A = 1000 ((1 + 0, 05 / 12) 12 - 1)
- A = 1000 ((1 + 0, 0042) 12 - 1)
- A = 1000 ((1.0042) 12 - 1)
- A = 1000 (1.0516 - 1)
- A = 1000 (0, 0516)
- A = 51, 6
Am calculat rata dobânzii timp de 1 an prin compunere lunară ca aproximativ 51, 6
Dobânda compusă lunară nu reflectă modificări notabile atunci când parchemăm o anumită sumă de bani pe termen scurt. Motivul este că este nevoie de câțiva ani pentru compunere pentru a produce schimbări vizibile în vigoare.
Și cel mai proeminent lucru despre interesul compus este că face ca investițiile dvs. să crească mai repede decât simpla dobândă. Cu cât este mai frecvent intervalul de compunere, cu atât este mai mare diferența sau putem spune că dobânda combinată zilnică generează mai mult venit din investițiile dvs. decât dobânda compusă anuală pentru orice rată a dobânzii dată.
Următorul tabel arată diferența pe care numărul perioadelor de compunere o poate face într-o anumită perioadă de timp pentru un împrumut de 10.000 USD, cu o dobândă anuală de 10% pe o perioadă de 12 ani.
| Frecvența compusă | Nr. Perioade compuse | Valori pentru i și n | Interes total |
| Anual | 1 | I = 10%, n = 12 | $ 21, 384.2837 |
| Semi anual | 2 | I = 5%, n = 24 | $ 22, 250.9994 |
| Trimestrial | 4 | I = 2, 5%, n = 48 | $ 22, 714.8956 |
| Lunar | 12 | I = 0, 833%, n = 144 | $ 23, 036.4896 |
Relevanța și utilizările formulei lunare de dobândă compusă
Interesul compus a dovedit un instrument mai bun pentru investiții, dar poate fi foarte periculos dacă este aplicabil pentru valoarea creditului dumneavoastră. Veți ajunge să plătiți mai multe dobânzi la suma împrumutului dvs.
Compunerea devine mai eficientă atunci când investiția dvs. este lunară sau trimestrială în loc de an, deoarece dă un randament mai bun. Dacă împrumutați bani de la oricare dintre bănci sau instituții financiare decât combinarea anuală este cea mai bună opțiune. Când împrumutați o anumită sumă de bani, combinarea zilnică va fi mai productivă. Dar trebuie să ținem cont, combinarea poate depinde favorabil sau nefavorabil de circumstanțe.
Dobânda compusă dă un profit mai bun asupra investiției dvs., depinde de mandatul și dimensiunea investiției. Interesul compus crește mai repede decât așteptările.
Beneficiile dobânzii compuse sunt enumerate mai jos:
- reinvestirea
- O mai bună rentabilitate a investiției.
- Economii pe termen lung.
- Câștiguri sporite
Calculator lunar cu formula dobânzii compuse
Puteți utiliza următorul Calculator lunar cu formulă de dobândă compusă
| P | |
| R | |
| T | |
| Formula dobânzii compuse lunare | |
| Formula dobânzii lunare compuse = | P x ((1 + R / 12) 12 * t - P) |
| = | 0 x ((1 +0/12) 12 * 0 - 0) = 0 |
Articole recomandate
Acesta este un ghid pentru formula lunară de dobândă compusă. Aici vom discuta despre cum să calculăm Formula de dobândă compusă lunară împreună cu exemple practice. Oferim, de asemenea, un calculator lunar al dobânzii compuse cu un șablon excel descărcabil. De asemenea, puteți consulta următoarele articole pentru a afla mai multe -
- Formula pentru rata anuală de creștere compusă
- Cum se calculează rata dobânzii nominale?
- Formula de dobândă compusă zilnică
- Ghid pentru formula Poisson Distribution
- Dobânda vs. Dividend | Top 8 diferențe cheie pe care ar trebui să le știi