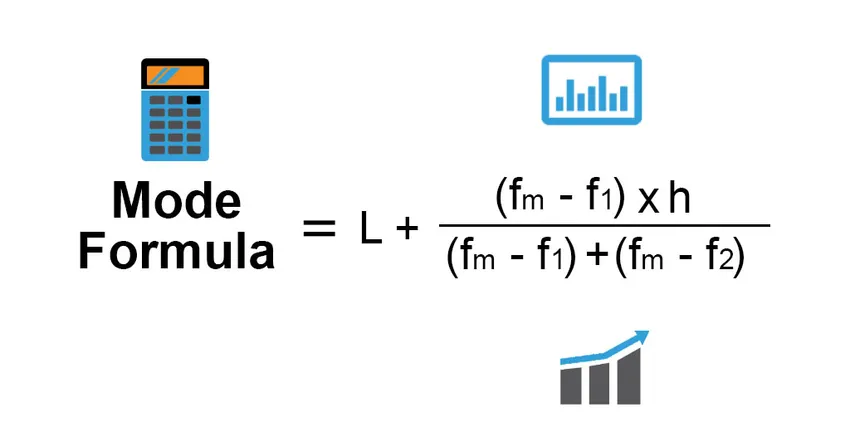
Formula modului (cuprins)
- Formulă
- Exemple
- Calculator
Ce este Formula Modului?
Cele trei măsuri centrale ale tendinței sunt mediul mediu și modul. Când toate cele trei sunt folosite împreună pentru a extrage analize semnificative din setul de date. Astăzi în acest articol vom discuta despre modul care este, de asemenea, una dintre tastele și importanta tendință centrală a metodei utilizate. Modul se referă la cea mai frecvent întâlnită valoare din setul de date. Modul unei date poate fi găsit cu setul de date normale, setul de date grup, precum și setul de date neagrupate sau neagrupate. Cu toate acestea, media utilizată cel mai frecvent rămâne totuși cea mai bună măsură a tendinței centrale, în ciuda existenței mediei, mediei și modului. În acest articol, vom încerca să înțelegem funcția modului, exemplele și explicațiile fiecărui exemplu, împreună cu formula și calculele.
Formula pentru modul este: -
Mode = L + (fm−f1)h /(fm−f1)+(fm−f2)
Formula de mod pentru date grupate:
Mod = L + (fm − f1) h / 2fm − f1 − f2
Unde,
- L = Limita inferioară Modul clasei modale
- fm = Frecvența clasei modale
- f1 = Frecvența clasei anterioare clasei modale
- f2 = Frecvența clasei care succede clasei modale
- h = Mărimea intervalului de clasă
Exemple de formulă de mod (cu șablon Excel)
Să luăm un exemplu pentru a înțelege calculul modului într-o manieră mai bună.
Puteți descărca acest șablon Formula de modul modul aici - Modulul Excel Formula modulFormula modului - Exemplul # 1
În cazul în care modul este calculat pur și simplu numărul de observații dintr-un set de date care are loc de cele mai multe ori.
Calculați modul următorului set de date.
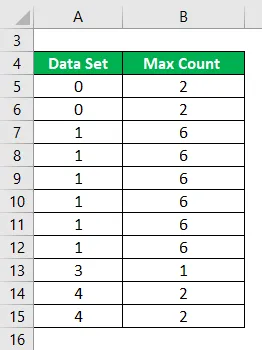
Soluţie:
Un mod este calculat ca:
Număr de observații dintr-un set de date care se petrece de cele mai multe ori
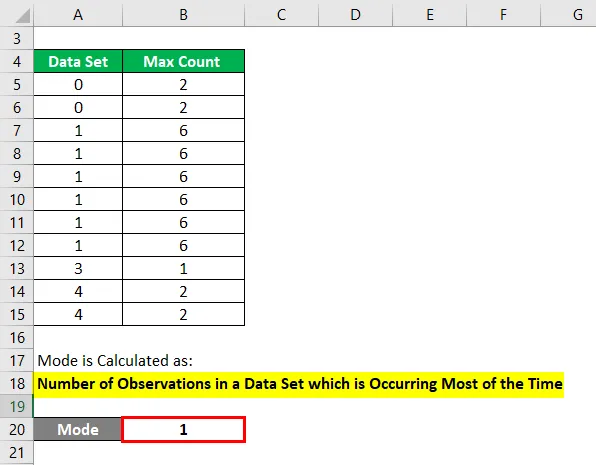
- Mod = 1
Formula modului - Exemplul # 2
Calculați modul utilizând informațiile date.
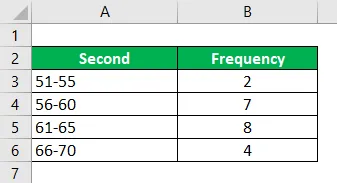
Soluţie:
Notă: - În primul rând, grupul modal cu cea mai mare frecvență trebuie să identifice Dacă intervalul nu este continuu, 0, 5 trebuie scăzut din modul limită inferioară și 0, 5 ar trebui adăugat din modul limită superioară. Atunci intervalul va fi
Grupul Modal este calculat ca:
Grupul modal care este cel mai frecvent adică 60, 5-65, 5
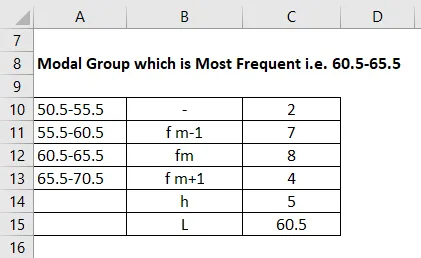
Atunci frecvența mai mică este a grupului modal, care este 4, în acest caz, este luat ca fm + 1 și fm-1 va deveni 7 în acest exemplu. Și avem fm care este frecvența ca 8. H (se numește) Mărimea intervalului de clasă este 5 pe care avem în vedere și intervalul de pornire. L este 60, 5.
Modul este calculat folosind formula dată mai jos
Mod = L + (fm − f1) h / (fm − f1) + (fm − f2)
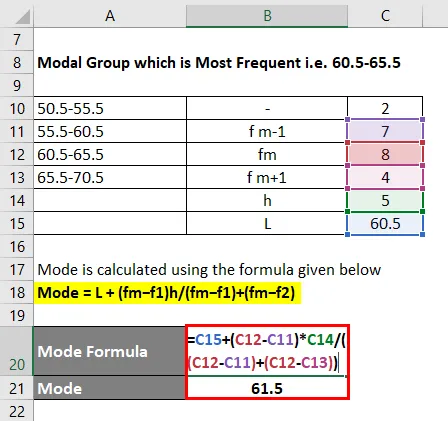
- Mod = 60, 5 + (8 - 7) * 5 / ((8 - 7) + (8 - 4))
- Mod = 61.5
Formula modului - Exemplul # 3
Următoarele sunt distribuțiile înălțimilor într-o anumită clasă de elevi într-un anumit Mod
Calculați modul utilizând informațiile date.
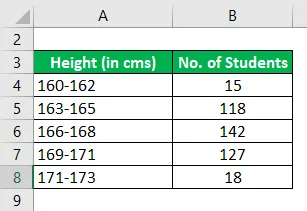
Soluţie:
Dacă intervalul nu este continuu, 0, 5 trebuie scăzute din modul limită inferioară și 0, 5 trebuie adăugate din modul limită superioară. Atunci intervalul va fi
Grupul Modal este calculat ca:
Grupul modal care este cel mai frecvent adică 165.5-168.5
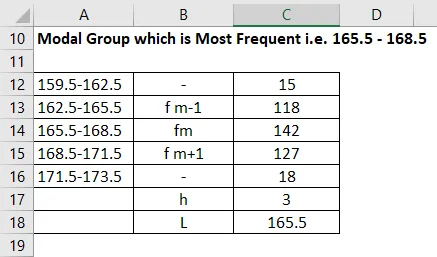
Modul este calculat folosind formula dată mai jos
Mod = L + (fm − f1) h / (fm − f1) + (fm − f2)
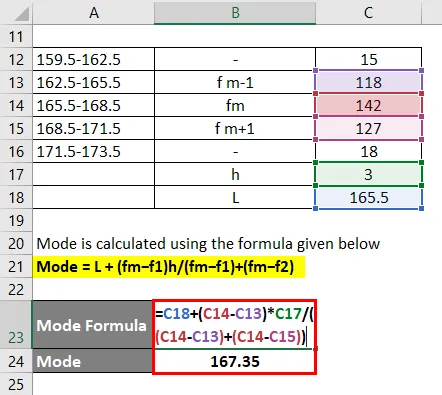
- Mod = 165, 5 + (142 - 118) * 3 / (142 - 118) + (142 - 127)
- Mod = 167.35
Explicaţie
Modul poate fi simplu explicat ca fiind valoarea care apare cel mai frecvent în setul de date. Și modul de mai sus poate fi explicat că atunci când datele sunt un grup, trebuie să calculăm mai întâi funcția modală și să facem datele continue pentru a calcula modul de date. Clasa modală este decisă cu clasa care are cea mai mare frecvență în setul de date.
Formula relevanței și utilizărilor modului
- Media, mediul și modul dezvăluie diferite aspecte ale datelor dvs. Oricine vă va oferi o idee generală, dar vă poate induce în eroare; având toate trei vă va oferi o imagine mai completă
- Pentru o distribuție normală, modul, media, mediana au aceeași valoare, deoarece Mode este o distribuție normală. Modul de analiză în mod izolat nu reflectă imaginea adevărată, dacă doriți să analizați setul complet de date, atunci toate cele trei măsuri statistice trebuie analizate în detaliu și interpretate
- Modul este ușor de înțeles și simplu de calculat.
- Modul nu este afectat de valori extrem de mari sau mici.
- Modul poate fi localizat doar prin inspecție în date neagrupate și distribuție de frecvență discretă.
- Modul poate fi util pentru date calitative.
- Modul poate fi calculat într-un tabel de frecvențe open-end.
- Modul poate fi localizat grafic
- Modul este folosit de oamenii de știință de date cel mai frecvent
- Modul este că nu ne va oferi o măsură foarte bună a tendinței centrale atunci când marca cea mai comună este departe de restul datelor din setul de date
Calculator de formulă de mod
Puteți utiliza următorul Calculator de formulă de mod
| L | |
| fm | |
| f1 | |
| F2 | |
| h | |
| Formula modului | |
| Formula modului = | L + (fm - f1) xh / (fm - f1) + (fm - f2) |
| = | 0 + (0 - 0) x 0 / (0 - 0) + (0 - 0) = 0 |
Articole recomandate
Acesta este un ghid pentru Formula Modului. Aici vom discuta despre cum să calculăm Formula Modului împreună cu exemple practice. De asemenea, oferim un calculator Mode cu un șablon excel descărcabil. De asemenea, puteți consulta următoarele articole pentru a afla mai multe -
- Exemple de formulă a modelului Gordon Growth
- Formula pentru calcularea modelului de preț al activelor de capital
- Calculator pentru formula raportului de cheltuieli totale
- Formula de distribuție Poisson (exemple cu șablon Excel)