
Introducere în funcția recursivă în Java
O funcție recursivă este cea care se numește de una sau de mai multe ori. O funcție recursivă este utilizată în situațiile în care același set de operații trebuie să fie efectuate din nou și din nou până la atingerea rezultatului. Efectuează mai multe iterații, iar declarația problemă continuă să devină mai simplă cu fiecare iterație.
Întotdeauna trebuie specificată o limită de bază în timpul scrierii unei funcții recursive, altfel are ca rezultat o eroare Stack Overflow. Un stivă este o zonă de memorie rezervată pentru a menține invocările metodei. Eroarea se datorează faptului că funcția începe să se execute continuu, deoarece nu va putea găsi condiția de limitare și, prin urmare, va epuiza memoria alocată. Deci, pentru a preveni overflow-ul Stack-ului, definim anumite condiții de bază cu ajutorul instrucțiunilor „if… else” (sau orice alte declarații condiționale), care face ca funcția de recurs să se oprească imediat ce calculul necesar este finalizat.
Tipuri de recursură în Java
Există 2 tipuri de recursiune în Java. Sunt:
1. Recursiune directă
Sintaxă:
Aici funcția1 se numește continuu, deci este o funcție recursivă.
public static void main(String() args)(
//few lines of code
function();
//few lines of code
)
function() (
//few lines of code
function();
//few lines of code
)
Exemplu
Factorialul unui număr este un exemplu de recursivitate directă. Principiul de bază al recursului este rezolvarea unei probleme complexe prin împărțirea în cele mai mici. De exemplu, în cazul factorial al unui număr, calculăm factorialul lui „i” dacă îl cunoaștem factorialul lui „i-1”.
Cod:
public class Factorial (
static int fact(int i)(
if (i == 1)
return 1;
else
return(i * fact(i-1));
)
public static void main(String() args) (
System.out.println("The factorial of given number 6 is: "+fact(6));
)
)
ieşire:

2. Recursiune indirectă / reciprocă
O funcție1 care apelează o altă funcție2, care la rândul său apelează funcție1 direct sau indirect se numește funcție indirectă recursivă.
Sintaxă:
Luați în considerare 2 funcții numite funcție1 () și funcție2 (). Aici funcția1 apelează funcția2 și funcția2 apelează funcția1.
function1()(
//few lines of code
function2();
//few lines of code
)
function2()(
//few lines of code
function1();
//few lines of code
)
Exemplu
Pentru a arăta recurenta indirectă, folosim următorul program folosit pentru a afla dacă un anumit număr este egal sau par din intrarea dată.
Cod:
import java.util.Scanner;
public class IndirectRecursion (
public static boolean oddNum(int i) (
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0)(
return false;
) else (
return evenNum(i-1);
)
)
public static boolean evenNum(int i) (
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0)(
return true;
) else (
return oddNum(i-1);
)
)
public static void main(String() args) (
Scanner inputNum = new Scanner(System.in);
System.out.print("Give a number: ");
int n = inputNum.nextInt();
if (evenNum(n)) System.out.println(n + " is even");
else System.out.println(n + " is odd");
inputNum.close();
)
)
ieşire:
Exemple de recurs în Java
Iată câteva exemple pentru rezolvarea problemelor folosind metoda de recurs.
Exemplul nr. 1 - Secvență de Fibonacci
Se spune că un set de numere „n” se află într-o secvență Fibonacci dacă numărul3 = număr1 + număr2, adică fiecare număr este o sumă a celor două numere precedente. Prin urmare, secvența începe întotdeauna cu primele două cifre precum 0 și 1. Cea de-a treia cifră este o sumă de 0 și 1 rezultând 1, al patrulea număr este adăugarea de 1 și 1 rezultând 2, iar secvența continuă.
Consultați următorul cod din Java pentru a genera o secvență Fibonacci:
public class FibonacciSeries(
static int num1=0, num2=1, num3=0;
static void fibonacci(int n)(
if(n>0)(
num3 = num1 + num2;
num1 = num2;
num2 = num3;
System.out.print(" "+num3);
fibonacci(n-1);
)
)
public static void main(String args())(
int n=10;
System.out.print(num1+" "+num2);//printing constant first two digits 0 and 1
fibonacci(n-2);//Since first two numbers are already done
)
)
ieşire:

Aici primele două numere sunt inițializate la 0 și 1 și sunt tipărite. Variabilele „num1”, „num2” și „num3” sunt utilizate pentru a genera secvența necesară. Variabila „num3” este obținută prin adăugarea „num1” și „num2”, iar numerele sunt mutate cu o poziție spre stânga, amestecând așa cum se arată în cod. Funcția „Fibonacci” este numită recursiv aici și la fiecare iterație, valoarea lui „n” este scăzută cu 1. Prin urmare, recursivitatea iese imediat ce „n” atinge valoarea 0.
Exemplul # 2 - Turnul Hanoiului
Aceasta este o problemă matematică clasică, care are 3 poli și un număr de „discuri” de discuri cu dimensiuni diferite. Puzzle-ul merge după cum urmează:
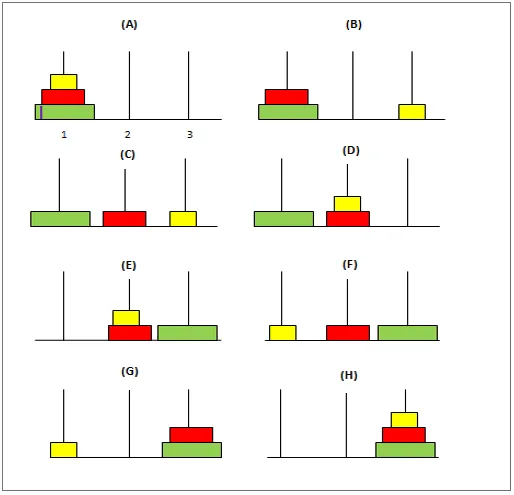
La început, primul pol va avea discurile aranjate astfel încât cel mai mare disc dintre toate să fie în partea de jos și cel mai mic în partea de sus a polului. Obiectivul este de a muta aceste discuri de la primul pol la al treilea pol, păstrând discurile în aceeași poziție ca cea din primul. Următoarele sunt câteva condiții de care trebuie să țineți cont în timp ce schimbați aceste discuri:
1. La un moment dat, un singur disc trebuie să fie mutat.
2. În acest proces, nu este permisă plasarea unui disc mai mare peste unul mai mic.
3. Al doilea pol (mijloc) poate fi utilizat pentru a media în timp ce transferați discurile de la primul la al doilea pol.
Urmează codul Java care poate fi utilizat pentru a rezolva puzzle-ul:
Cod:
public class TowerOfHanoi (
public static void main(String() args) (
int count = 3;
tower(count, 'A', 'B', 'C');
)
public static void tower(int first, char disk1, char temp, char disk2) (
if (first == 1) (
System.out.println("Disk 1 from " + disk1 + " to " + disk2);
) else (
tower(first - 1, disk1, disk2, temp);
System.out.println("Disk " + first + " from " + disk1 + " to " + disk2);
tower(first - 1, temp, disk1, disk2);
)
)
)
ieşire:
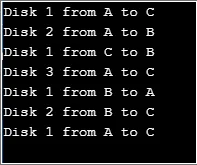
Aici variabila „număr” reprezintă numărul de discuri folosite. Funcția „turn” este funcția recursivă folosită pentru deplasarea discurilor de la tija 1 la tija 3. O soluție simplă la această problemă poate fi furnizată luând în considerare 2 discuri la început.
- În primul rând, începem prin mutarea disc1 de la tija 1 la tija 2.
- În continuare, mutăm disc2 pe tija 3.
- În cele din urmă, terminăm prin mutarea disc1 la tija 3 completând soluția necesară.
Același principiu este aplicat pentru numărul „n” de discuri mutând (n-1) discul de la tija 1 la 2 și urmând pași similari ca mai sus.
Avantajele recursiunii în Java
- Codul este ușor de scris și de întreținut.
- Cea mai bună metodă de a găsi rezultatele în care este necesar un număr mare de iterații.
Dezavantajele recurentei în Java
- Funcțiile recursive folosesc mai multă memorie. Acest lucru se datorează faptului că de fiecare dată este apelată o funcție recursivă; alocarea memoriei se face recent pentru variabilele din stivă. Și alocarea de memorie respectivă este eliberată imediat ce valorile variabile sunt returnate.
- Acest proces de alocare a memoriei durează mai mult timp, de aceea execuția este de obicei lentă.
Concluzie
Funcțiile recursive sunt relativ mai simple de codat, dar nu sunt atât de eficiente în comparație cu celelalte metode existente. Prin urmare, acestea sunt utilizate mai ales în cazurile în care timpul acordat dezvoltării este mai mic și, de asemenea, în cazul în care un model semnificativ poate fi observat în problemă.
Articole recomandate
Acesta este un ghid pentru Recursiune în Java. Aici discutăm tipurile de Recursiune în Java împreună cu diferitele sale exemple cu avantajele și dezavantajele. De asemenea, puteți consulta următoarele articole pentru a afla mai multe-
- JScrollPane în Java
- Funcții matematice în Java
- Funcții matematice în Java
- Constructor în Java
- Funcția recurentă în Python
- Programul factorial în JavaScript