Definiția Mean Shift Algorithm
Algoritmul Shift Mean se încadrează în învățarea nesupravegheată, care este clasificată ca algoritmul Clustering. Ideologia algoritmului de schimbare medie este aceea că acesta atribuie în mod iterativ puncte de date clusterelor prin trecerea către punctul care are cel mai mare punct de densitate (Mod). Logica care stă la baza schimbării medii se bazează pe conceptul de estimare a densității Kernel, denumit KDE.
Gruparea algoritmului de schimbare medie
O tehnică de învățare nesupervizată descoperită de Fukunaga și Hostetler pentru a găsi clustere:
- Mean Shift este, de asemenea, cunoscut ca algoritmul de căutare a modului care atribuie punctele de date clusterelor într-un mod prin mutarea punctelor de date către regiunea cu densitate înaltă. Cea mai mare densitate a punctelor de date este denumită model în regiune. Algoritmul Mean Shift are aplicații utilizate pe scară largă în domeniul viziunii computerizate și segmentarea imaginilor.
- KDE este o metodă de estimare a distribuției punctelor de date. Funcționează prin plasarea unui nucleu pe fiecare punct de date. Nucleul în termeni matematici este o funcție de ponderare care va aplica greutăți pentru punctele de date individuale. Adăugarea întregului nucleu generează probabilitatea.
Funcția Kernel trebuie să îndeplinească următoarele condiții:
- Prima cerință este să se asigure că estimarea densității nucleului este normalizată.
- A doua cerință este ca KDE să fie bine asociat cu simetria spațiului.
Două funcții populare de kernel
Mai jos sunt cele două funcții populare ale kernel-ului utilizate în acestea:
- Kernel plat
- Kernel gaussian
- Pe baza paramei Kernel utilizate, densitatea rezultată variază. Dacă nu este menționat niciun parametru de kernel, Kernel Gaussian este invocat implicit. KDE utilizează conceptul de funcție a densității probabilității care ajută la găsirea maximelor locale ale distribuției datelor. Algoritmul funcționează făcând ca punctele de date să se atragă reciproc, permițând punctele de date către zona cu densitate ridicată.
- Punctele de date care încearcă să convergă către maximele locale vor fi din același grup de cluster. Spre deosebire de algoritmul de aglomerare K-Means, rezultatul algoritmului „Shift Mean” nu depinde de presupunerile legate de forma punctului de date și de numărul de clustere. Numărul de clustere va fi determinat de algoritm cu privire la date.
- Pentru a efectua implementarea algoritmului Mean Shift, folosim pachetul python SKlearn.
Implementarea algoritmului de schimbare medie
Mai jos este implementarea algoritmului:
Exemplul # 1
Bazat pe Tutorialul Sklearn pentru Algoritmul Clusteringului Climatizării Medii. Primul fragment va implementa un algoritm de schimbare medie pentru a găsi grupurile setului de date bidimensional. Pachetele utilizate pentru implementarea algoritmului de schimbare medie.
Cod:
fromcluster importMeanShift, estimate_bandwidth
from sklearn.datasets.samples_generator import make_blobs as mb
importpyplot as plt
fromitertools import cycle as cy
Un lucru cheie de remarcat este că vom folosi biblioteca make_blobs de la sklearn pentru a genera puncte de date centrate pe 3 locații. Pentru a aplica algoritmul shift shift pe punctele generate, trebuie să stabilim lățimea de bandă care reprezintă interacțiunea dintre lungime. Biblioteca lui Sklearn are funcții încorporate pentru a estima lățimea de bandă.
Cod:
#Sample data points
cen = ((1, .75), (-.75, -1), (1, -1)) x_train, _ = mb(n_samples=10000, centers= cen, cluster_std=0.6)
# Bandwidth estimation using in-built function
est_bandwidth = estimate_bandwidth(x_train, quantile=.1,
n_samples=500)
mean_shift = MeanShift(bandwidth= est_bandwidth, bin_seeding=True)
fit(x_train)
ms_labels = mean_shift.labels_
c_centers = ms_labels.cluster_centers_
n_clusters_ = ms_labels.max()+1
# Plot result
figure(1)
clf()
colors = cy('bgrcmykbgrcmykbgrcmykbgrcmyk')
fori, each inzip(range(n_clusters_), colors):
my_members = labels == i
cluster_center = c_centers(k) plot(x_train(my_members, 0), x_train(my_members, 1), each + '.')
plot(cluster_center(0), cluster_center(1),
'o', markerfacecolor=each,
markeredgecolor='k', markersize=14)
title('Estimated cluster numbers: %d'% n_clusters_)
show()
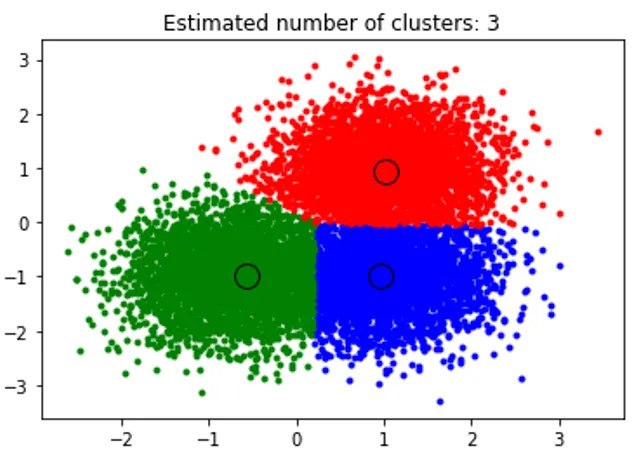
Snippet-ul de mai sus realizează clustering și algoritmul a găsit clustere centrate pe fiecare bloc pe care l-am generat. Putem vedea că din imaginea de mai jos, trasată de fragment, este prezentat algoritmul de schimbare medie, capabil să identifice numărul de grupuri necesare în timpul de rulare și să descopere lățimea de bandă corespunzătoare pentru a reprezenta lungimea interacțiunii.
ieşire:
Exemplul # 2
Bazat pe Segmentarea imaginii în viziunea computerului. Al doilea fragment va explora modul în care algoritmul de schimbare medie utilizat în învățarea profundă pentru a realiza segmentarea imaginii colorate. Folosim algoritmul „Shift Mean” pentru a identifica grupurile spațiale. Fragmentul anterior am folosit setul de date 2-D, în timp ce în acest exemplu vom explora spațiul 3-D. Pixelul imaginii va fi tratat ca puncte de date (r, g, b). Trebuie să convertim imaginea în format matriciu, astfel încât fiecare pixel să reprezinte punctul de date din imaginea pe care o ducem la segment. Gruparea valorilor culorii în spațiu returnează o serie de clustere, în care pixelii din cluster vor fi similari cu spațiul RGB. Pachetele utilizate pentru implementarea algoritmului de schimbare medie
Cod:
importnumpy as np
fromcluster importMeanShift, estimate_bandwidth
fromdatasets.samples_generator importmake_blobs
importpyplot as plt
fromitertools import cycle
fromPIL import Image
Mai jos Snippet pentru a realiza segmentarea imaginii originale:
#Segmentation of Color Image
img = Image.open('Sample.jpg.webp')
img = np.array(img)
#Need to convert image into feature array based
flatten_img=np.reshape(img, (-1, 3))
#bandwidth estimation
est_bandwidth = estimate_bandwidth(flatten_img,
quantile=.2, n_samples=500)
mean_shift = MeanShift(est_bandwidth, bin_seeding=True)
fit(flatten_img)
labels= mean_shift.labels_
# Plot image vs segmented image
figure(2)
subplot(1, 1, 1)
imshow(img)
axis('off')
subplot(1, 1, 2)
imshow(np.reshape(labels, (854, 1224)))
axis('off')
Imaginea generată afirmă că această abordare pentru a identifica formele imaginilor și a determina grupurile spațiale se poate efectua fără o prelucrare a imaginii.
ieşire:


Beneficii și aplicații Algoritmul schimbării medii
Mai jos sunt avantajele și aplicarea algoritmului mediu:
- Este utilizat pe scară largă pentru a rezolva viziunea computerului, unde este utilizat pentru segmentarea imaginii.
- Gruparea punctelor de date în timp real, fără a menționa numărul de clustere.
- Funcționează bine în segmentarea imaginilor și urmărirea video.
- Mai robuste în evidență.
Beneficiile algoritmului de schimbare medie
Mai jos sunt algoritmii de schimbare medie a avantajelor:
- Rezultatul algoritmului este independent de inițializări.
- Procedura este eficientă, deoarece are un singur parametru - Lățimea de bandă.
- Fără ipoteze privind numărul de grupuri de date și forma.
- Are o performanță mai bună decât K-Means Clustering.
Contra algoritmului de schimbare medie
Mai jos sunt contra de algoritmul de schimbare medie:
- Scump pentru funcții mari.
- În comparație cu gruparea K-Means este foarte lent.
- Ieșirea algoritmului depinde de lățimea de bandă a parametrilor.
- Ieșirea depinde de dimensiunea ferestrei.
Concluzie
Deși este o abordare simplă, care a fost utilizată în principal pentru rezolvarea problemelor legate de segmentarea imaginilor, clustering. Este relativ mai lent decât K-Means și este costisitor din punct de vedere al calculului.
Articole recomandate
Acesta este un ghid pentru algoritmul de schimbare medie. Aici discutăm problemele legate de segmentarea imaginii, clustering, beneficii și două funcții Kernel. Puteți, de asemenea, să parcurgeți alte articole conexe pentru a afla mai multe-
- K- Înseamnă algoritmul de clustering
- Algoritmul KNN în R
- Ce este algoritmul genetic?
- Metode de kernel
- Metode de nucleu în învățarea mașinii
- Detaliu Explicația algoritmului C ++