
Introducere în seria Fibonacci din Python
Seria Fibonacci din Python, aceasta este denumită o serie de numere, unde următorul număr este suma celor două numere prezente.
De exemplu:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 ..so on
Deci aici 0 + 1 = 1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
8+ 13 = 21 și așa mai departe.
Analizând cele de mai sus, cineva ar fi avut o idee sigură despre ce vorbim.
Cu toate acestea, În ceea ce privește regula matematică, poate fi scris ca:

În cazul în care numărul al șaptelea este suma numărului în locuri (n-1) și (n-2). Când vine vorba de implementarea seriei Fibonacci, ar putea exista o serie de limbaje de codare prin intermediul cărora ar putea fi realizată.
Cu toate acestea, Python este un limbaj larg utilizat în zilele noastre. Să vedem implementarea seriei Fibonacci prin Python. Unul ar trebui să fie conștient de afirmațiile de condiționare de bază, precum bucla, dacă-altfel, în timp ce buclă, etc. în Python, înainte de a continua aici. În caz contrar, ar fi minunat dacă îl putem revizui și apoi vom prelua conținutul care vine. Aici, în scop demo, folosesc spyder care este IDE pentru limbajul de programare python. Puteți utiliza orice alte notebook-uri IDE sau Ipython pentru execuția programelor Python.
Seria Fibonacci din Python
Să vedem punerea în aplicare a numărului Fibonacci și a seriei, luând în considerare primul element al Fibonacci sunt 0 și 1:
Cu toate acestea, puteți regla funcția Fibonacci conform cerințelor dvs., dar vedeți elementele de bază mai întâi și treceți treptat la altele.
Cod Python pentru găsirea celui de-al nouălea număr Fibonacci
Cod 1:
def Fibonacci_num(m):
u = 0
v = 1
if m < 0:
print("Incorrect input entered")
elif m == 0:
return u
elif m == 1:
return v
else:
for i in range(2, m):
c = u + v
u = v
v = c
return v
Cod 2:
ieşire:
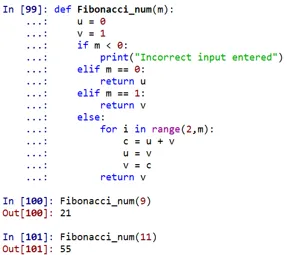
După cum se poate observa, numărul Fibonacci pe locul 9 ar fi 21, iar pe locul 11 ar fi 55.
- Aici „fibonacci_num” este o funcție definită, care are grijă să găsească numărul Fibonacci cu ajutorul anumitor condiții. Această funcție poate fi apelată specificând orice poziție.
Acum să vedem cum se pot tipări serii până la poziția menționată:
Cod:
ieşire:
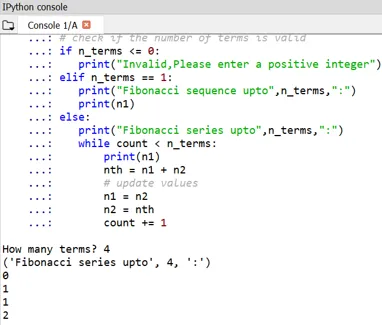
Se poate observa începutul numerelor Fibonacci este definit ca 0 și 1.
- Dacă cineva dorește să-și definească propriii termeni de pornire, acesta poate fi, de asemenea, realizat în același mod prin tweaking n1 și n2. Iată exemplul pentru asta:
Să spunem acum că vrem ca termenii noștri să fie: n1 = 3, n2 = 5
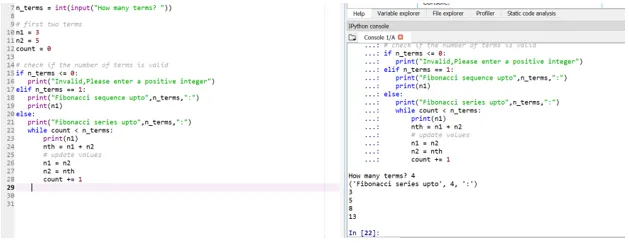
Așadar, aici poziția dvs. de-al patrulea termen (intrarea utilizatorului), va fi decisă pe baza termenilor de pornire.
Metode prin care se pot genera seria Fibonacci
Mai jos sunt prezentate cele trei metode prin care se pot genera seriile Fibonacci:
1. Prin intermediul generatoarelor
Cod:
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
ieşire:
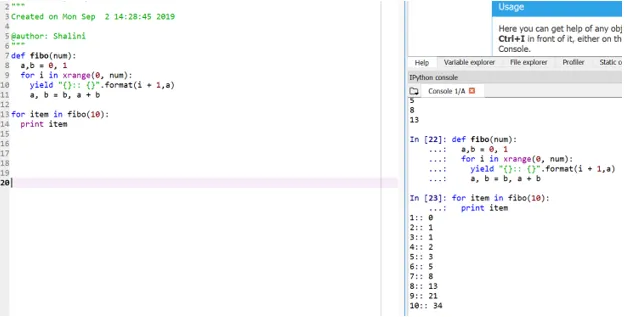
Această metodă este denumită „generator” deoarece funcția xrange este un generator al numerelor între 0 și num, iar randamentul este generatorul pentru ieșirea formatată.
Iată ce face xrange pentru tine:

Aici seria Fibonacci a fost definită sub forma funcției, în interiorul căreia pentru funcție buclă, xrange și randament are grijă de ieșire.
2. Prin buclă
Cod:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
ieşire:

După cum se poate vedea, simplă pentru buclă a fost utilizată, pentru a tipări seria Fibonacci între 0 până la 10. În interior pentru buclă, au fost alocate noi valori la variabile. U și v sunt valorile inițiale implicite ale Fibonacci care au fost setate la 0, respectiv 1.
În ceea ce privește bucla progresă pentru a rula, noua valoare u este valoarea veche v, în timp ce noua valoare v este suma valorilor vechi ale u și v. Aceasta continuă până la sfârșitul valorilor intervalului.
3. Prin recurs
Cod:
#Through recursion
def fibonacci_ser(m):
if(m <= 1):
return m
else:
return(fibonacci_ser(m-1) + fibonacci_ser(m-2))
m = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(m):
print fibonacci_ser(i),
ieşire:
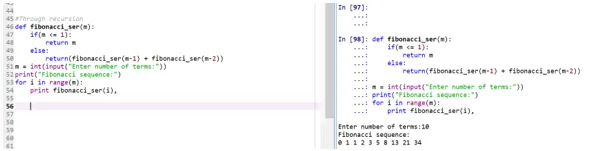
- Funcția „fibonacci_ser” face apelul la sine pentru a tipări seria Fibonacci.
- Prin urmare, metoda și-a primit numele de „recurs”.
Pași urmați aici:
- Aici utilizatorul a fost solicitat să introducă locul până la care trebuie să fie tipărită seria Fibonacci.
- Numărul trece prin funcția „fibonacci_ser”.
- Starea este verificată, dacă lungimea furnizată este mai mică de 1 sau nu. Dacă da, rezultatul este dat imediat.
- Cu toate acestea, dacă lungimea este mai mare de 1, apelurile recursive sunt efectuate către „fibonacci_ser” cu argumente care au lungimea mai mică de 1 și 2 adică fibonacci_ser (m-1) și fibonacci_ser (m-2).
- Prin urmare, recursivitatea oferă ieșirea dorită și o imprimă.
- Deci, pe scurt, am discutat Trei modalități de afișare a serialului Fibonacci.
- Prin buclă, prin generatoare și prin recurs.
Toate cele trei coduri Python sunt rezumate
Mai jos sunt prezentate cele trei coduri piton:
1. Prin intermediul generatoarelor
Cod:
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
2. Prin buclă
Cod:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
3. Prin recurs
Cod:
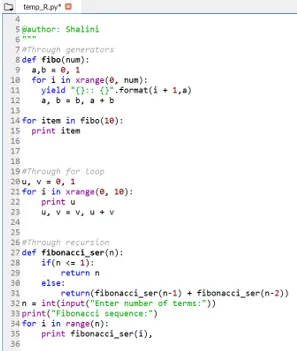
def fibonacci_ser(n):
if(n <= 1):
return n
else:
return(fibonacci_ser(n-1) + fibonacci_ser(n-2))
n = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(n):
print fibonacci_ser(i),
Rezumate mai sus sunt toate procedurile, trebuie să exersăm pentru a obține o aderență bună asupra tuturor.
ieşire:
Concluzie
Parcurgând conținutul de mai sus al Fibonacci, s-ar fi putut înțelege foarte clar numerele și seriile Fibonacci, specializate cu python. Odată, cineva se simte confortabil cu logica seriei Fibonacci, generând un alt set de serii, care lucrează cu alte numere și cu diferite metode va fi acum un tort pentru tine. O abordare logică este singura modalitate de a excela în acest sens.
Articole recomandate
Acesta este un ghid pentru seria Fibonacci din Python. Aici discutăm numerele și seriile Fibonacci, specializate cu python, generând un alt set de serii, care lucrează cu alte numere și cu diverse metode. Puteți parcurge și alte articole conexe pentru a afla mai multe -
- Generator de număr aleatoriu în Python
- Funcții matematice în Python
- Factorial în Python
- Încapsulare în Python
- Seria Fibonacci în Java
- Caracteristici Python
- Programul factorial în JavaScript
- Generator de număr aleatoriu în Matlab
- Generator de număr aleatoriu în C #
- Încapsulare în JavaScript