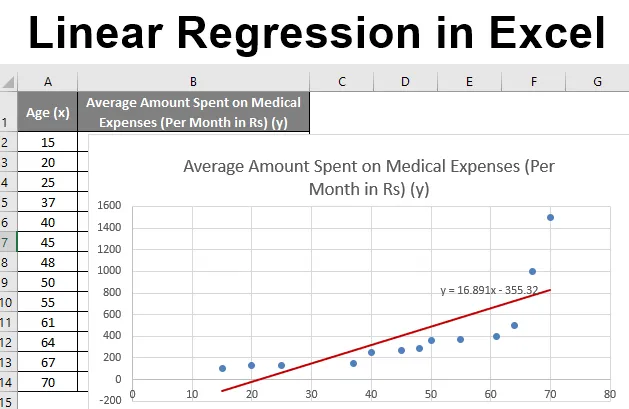
Regresie liniară în Excel - Cum se face regresia liniară în Excel?

Regresie liniară în Excel (cuprins)

Introducere în regresia liniară în Excel
Metode de utilizare a regresiei liniare în Excel

Introducere în regresia liniară în Excel

Regresia liniară este o tehnică / metodă statistică folosită pentru a studia relația dintre două variabile cantitative continue. În această tehnică, variabilele independente sunt utilizate pentru a prezice valoarea unei variabile dependente. Dacă există o singură variabilă independentă, atunci este o regresie liniară simplă și dacă un număr de variabile independente sunt mai mult decât una, atunci aceasta este regresie liniară multiplă. Modelele de regresie liniară au o relație între variabile dependente și independente, prin potrivirea unei ecuații liniare la datele observate. Linear se referă la faptul că folosim o linie pentru a se potrivi cu datele noastre. Variabilele dependente utilizate în analiza de regresie se mai numesc variabile de răspuns sau previzionate, iar variabilele independente sunt de asemenea numite variabile explicative sau predictori.

O linie de regresie liniară are o ecuație de genul: Y = a + bX;

Unde:

X este variabila explicativă,
Y este variabila dependentă,
b este panta liniei,
a este interceptarea y (adică valoarea lui y când x = 0).

Metoda celor mai mici pătrate este utilizată în general în regresia liniară care calculează linia cea mai potrivită pentru datele observate, reducând la minimum suma de pătrate de deviere a punctelor de date de la linie.

Metode de utilizare a regresiei liniare în Excel

Acest exemplu vă învață metodele pentru a efectua analiza de regresie liniară în Excel. Să ne uităm la câteva metode.

Puteți descărca acest șablon Excelent pentru regresie liniară aici - șablonul de regresie liniară

Metoda # 1 - Grafic Scatter cu un trend

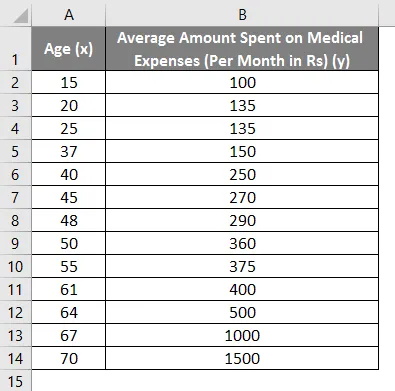
Să spunem că avem un set de date al unor persoane cu vârsta lor, indicele de masă bio (IMC) și suma cheltuită de aceștia pentru cheltuielile medicale într-o lună. Acum, cu o perspectivă asupra caracteristicilor indivizilor, cum ar fi vârsta și IMC, dorim să aflăm modul în care aceste variabile afectează cheltuielile medicale și, prin urmare, le folosim pentru a efectua regresia și a estima / prezice cheltuielile medicale medii pentru anumite persoane. Să vedem mai întâi cum afectează doar vârsta cheltuielile medicale. Să vedem setul de date:

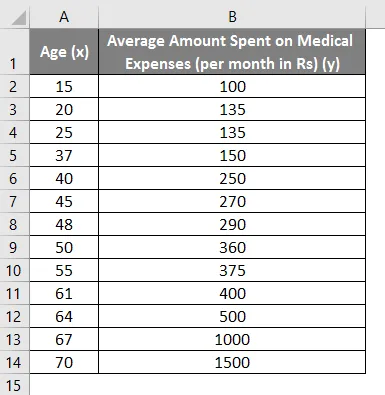
Suma cheltuielilor medicale = b * vârsta + a

Selectați cele două coloane ale setului de date (x și y), inclusiv anteturile.

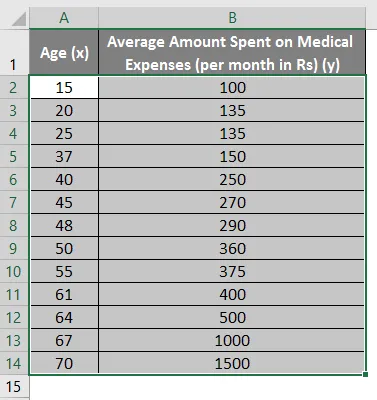
Faceți clic pe „Insert” și extindeți meniul vertical pentru „Graficul Scatter” și selectați miniatura „Scatter” (primul)

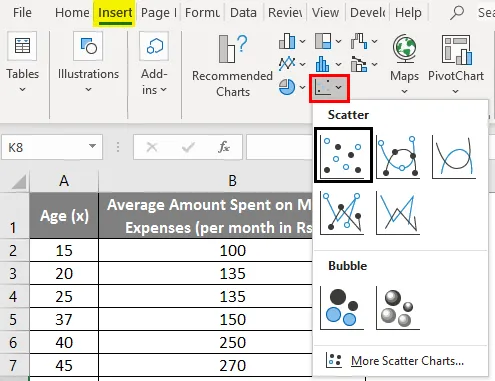
Acum va apărea un complot de dispersie și am trasa linia de regresie în acest sens. Pentru a face acest lucru, faceți clic dreapta pe orice punct de date și selectați „Adăugați trend”

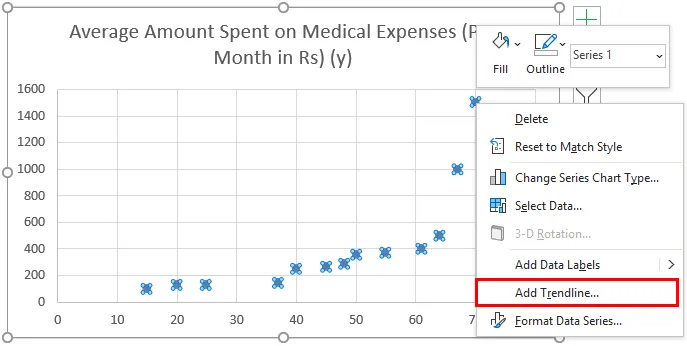
Acum, în panoul „Format Trendline” din dreapta, selectați „Line line Trendline” și „Display Equation on Chart”.

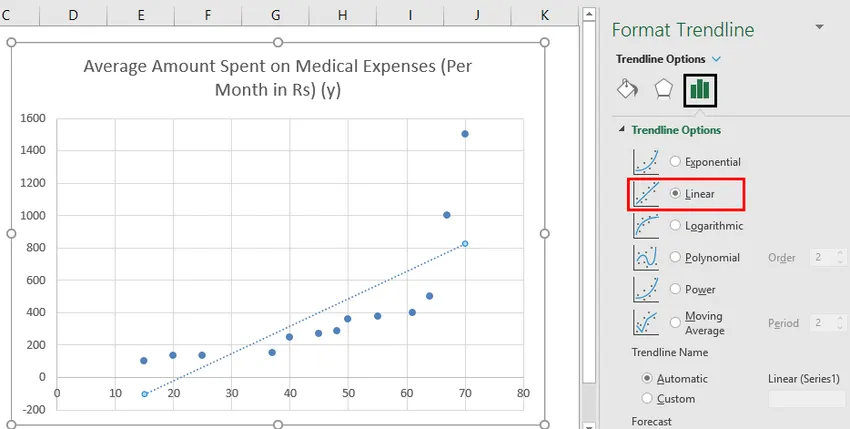
Selectați „Ecuație afișată pe grafic”.

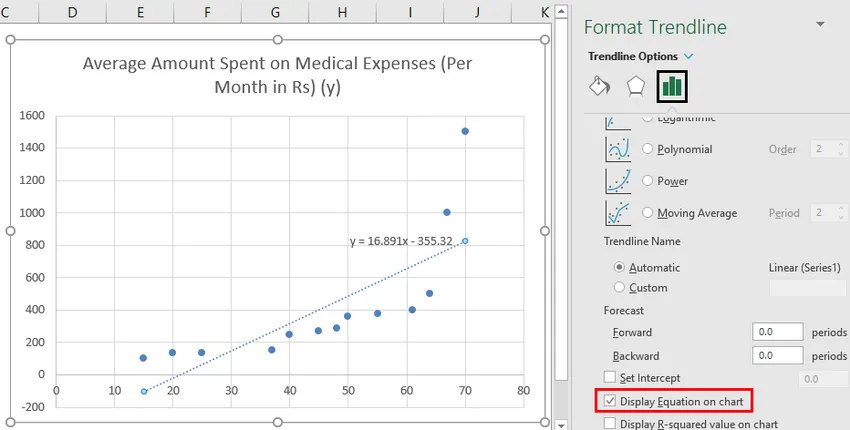
Putem improviza graficul conform cerințelor noastre, cum ar fi adăugarea titlurilor axelor, modificarea scării, culorii și tipului de linie.

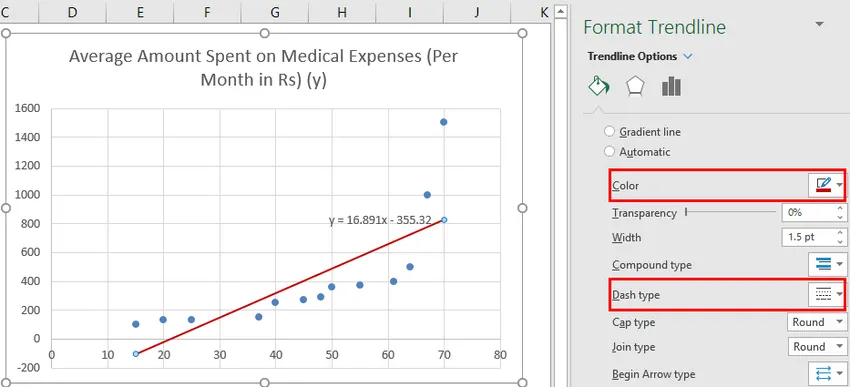
După improvizarea graficului, acesta este rezultatul pe care îl obținem.

Notă: În acest tip de grafic de regresie, variabila dependentă ar trebui să fie întotdeauna pe axa y, și independentă pe axa x. Dacă graficul este reprezentat în ordine inversă, atunci schimbați axele dintr-un grafic sau schimbați coloanele din setul de date.

Metoda 2 - Metoda suplimentară Instrument Toolkak de analiză

Uneori, Instrumentul de analiză nu este activat implicit și trebuie să îl facem manual. Pentru aceasta:

Faceți clic pe meniul „Fișier”.

După aceasta, faceți clic pe „Opțiuni”.

Selectați „Complementele Excel” în caseta „Gestionați” și faceți clic pe „Du-te”

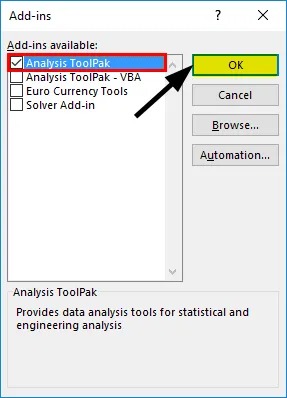
Selectați „Instrumentul de analiză” -> „OK”

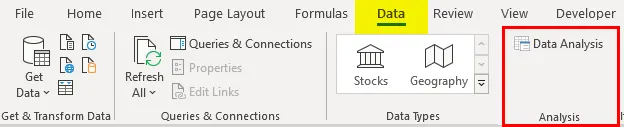
Acest lucru va adăuga instrumente „Analiza datelor” în fila „Date”. Acum rulăm analiza de regresie:

Faceți clic pe „Analiza datelor” din fila „Date”

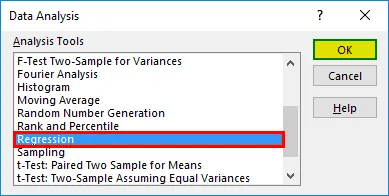
Selectați „Regresie” -> „OK”

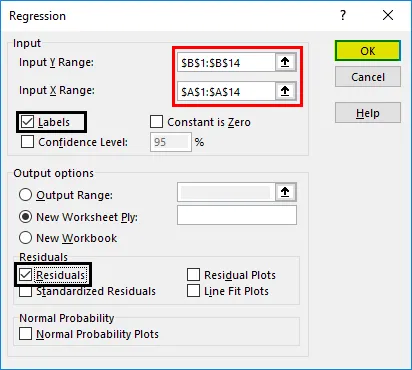
Va apărea o casetă de dialog cu regresie. Selectați intervalul de intrare Y și intervalul de intrare X (cheltuieli medicale și, respectiv, vârsta). În cazul regresiei liniare multiple, putem selecta mai multe coloane de variabile independente (cum ar fi dacă dorim să vedem impactul IMC și asupra cheltuielilor medicale).
Bifează caseta „Etichete” pentru a include anteturile.
Alegeți opțiunea dorită „ieșire”.
Selectați caseta de selectare „reziduuri” și faceți clic pe „OK”.

Acum, ieșirea noastră de analiză de regresie va fi creată într-o nouă foaie de lucru, în care se precizează Statisticile de regresie, ANOVA, reziduurile și coeficienții.

Interpretarea rezultatelor:

Statistica de regresie spune cât de bine se potrivește ecuația de regresie a datelor:

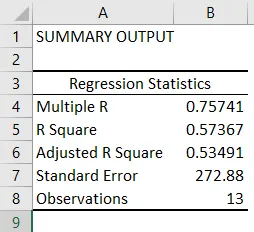
R multiplu este coeficientul de corelație care măsoară puterea relației liniare între două variabile. Se situează între -1 și 1, iar valoarea sa absolută prezintă puterea relației cu o valoare mare care indică o relație mai puternică, valoare scăzută indicând negativ și valoare zero care indică nicio relație.
R Square este coeficientul de determinare utilizat ca indicator al bunătății de potrivire. Se află între 0 și 1, cu o valoare apropiată de 1 care indică faptul că modelul este potrivit. În acest caz, 0, 57 = 57% din valorile y sunt explicate de valorile x.
R Square Square este R Square ajustat pentru numărul de predictori în caz de regresie liniară multiplă.
Eroarea standard prezintă precizia analizei de regresie.
Observațiile prezintă numărul de observații ale modelului.
Anova spune nivelul de variabilitate în cadrul modelului de regresie.

Acest lucru nu este utilizat în general pentru regresia liniară simplă. Cu toate acestea, „valorile F semnificative” indică cât de fiabile sunt rezultatele noastre, cu o valoare mai mare de 0, 05 sugerează alegerea unui alt predictor.

Coeficienții sunt partea cea mai importantă folosită pentru construirea ecuației de regresie.

Deci, ecuația noastră de regresie ar fi: y = 16.891 x - 355.32. Aceasta este aceeași cu cea făcută prin metoda 1 (diagramă de împrăștiere cu o linie de tendință).

Acum, dacă dorim să prezicem cheltuieli medicale medii, la vârsta de 72 de ani:

Deci y = 16.891 * 72 -355.32 = 860.832

Astfel, putem prezice valori ale y pentru orice alte valori ale lui x.

Reziduurile indică diferența dintre valorile reale și cele previzionate.

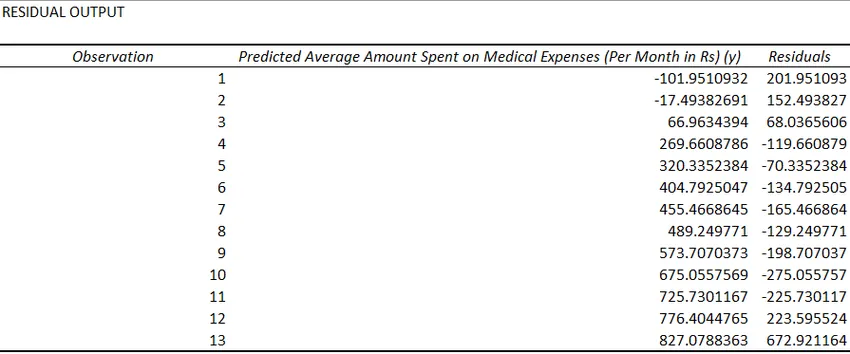
Ultima metodă de regresie nu este atât de frecvent utilizată și necesită funcții statistice precum panta (), interceptarea (), core () etc. pentru a realiza analiza de regresie.

Lucruri de reținut despre regresia liniară în Excel

Analiza de regresie este utilizată în general pentru a vedea dacă există o relație semnificativă statistic între două seturi de variabile.
Este utilizat pentru a prezice valoarea variabilei dependente pe baza valorilor uneia sau mai multor variabile independente.
Ori de câte ori dorim să încadrăm un model de regresie liniară la un grup de date, atunci intervalul de date trebuie observat cu atenție ca și cum am folosi o ecuație de regresie pentru a prezice orice valoare în afara acestui interval (extrapolare), atunci poate duce la rezultate greșite.

Articole recomandate

Acesta este un ghid pentru regresia liniară în Excel. Aici vom discuta despre cum se face regresia liniară în Excel, împreună cu exemple practice și șablonul excel descărcabil. De asemenea, puteți parcurge și alte articole sugerate -