
Introducere în funcții în R
Funcția este definită ca un set de declarații, pentru a efectua și îndeplini orice sarcină logică specifică. Funcția ia unii parametri de intrare care sunt cunoscuți ca argumente pentru a efectua acea sarcină. Funcțiile ajută la ruperea codului, în bucăți mai simple, orchestrându-l logic, ceea ce este mai ușor de citit și de înțeles. În acest subiect, vom afla despre Funcții în R.
Cum se scrie Funcții în R?
Pentru a scrie funcția în R, iată sintaxa:
Fun_name <- function (argument) (
Function body
)
Aici, se poate vedea cuvântul rezervat specific „funcție” este folosit în R, pentru a defini orice funcție. Funcția are intrare, care este sub formă de argumente. Corpul funcției este un set de enunțuri logice care sunt executate peste argumente și apoi returnează ieșirea. „Fun_name” este numele dat funcției, prin care poate fi apelat oriunde în programul R.
Să vedem un exemplu, care va fi mai lucid în înțelegerea conceptului de funcție în R.
Cod R
Multi <- function(x, y) (
# function to print x multiply y
result <- x*y
print(paste(x, "Multiply", y, "is", result))
)
ieșire:
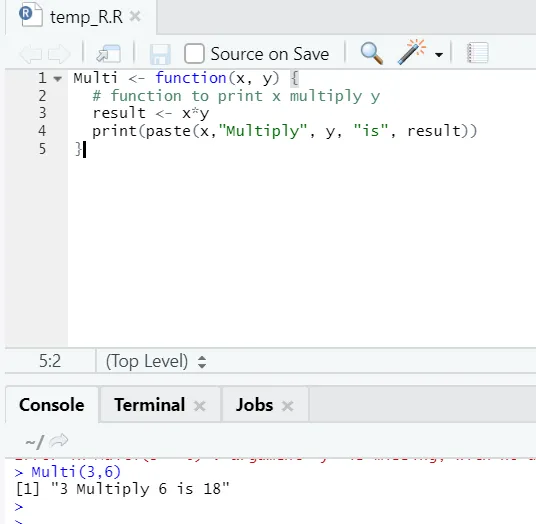
Aici am creat numele funcției „Multi”, care ia două argumente ca intrări și oferă ieșirea înmulțită. Primul argument este x și al doilea argument este y. După cum vedeți, am numit funcția cu numele „Multi”. Aici, dacă cineva dorește, argumentele pot fi setate și la valoarea implicită.
Diferite tipuri de funcții în R
Funcții R diferite cu sintaxă și exemple (încorporate, matematice, statistice etc.)
1) Funcție încorporată -
Acestea sunt funcțiile care vin cu R pentru a aborda o sarcină specifică, luând un argument ca intrare și oferind o ieșire bazată pe intrarea dată. Să discutăm câteva funcții generale importante ale lui R:
a) Sortare: datele pot fi de ordinul ascendent sau descendent. Datele pot fi dacă un vector de variabilă continuă sau variabilă de factor.
Sintaxă:

Iată explicația parametrilor săi:
- x: Acesta este un vector al variabilei continue sau al variabilei de factor
- în scădere: Aceasta poate fi setată fie Adevărat / Fals pentru a controla ordinea ascendentă sau descendentă. În mod implicit, este FALSE`.
- last: Dacă vectorul are valori NA, ar trebui să fie ultimul sau nu
Cod R și ieșire:
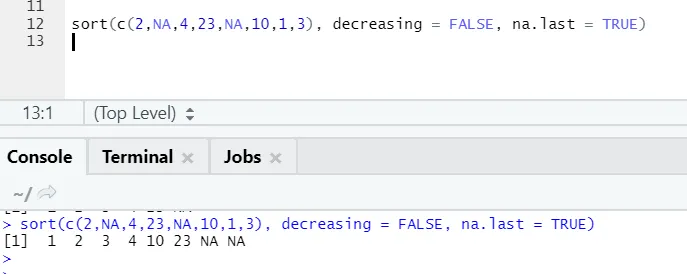
Aici se poate observa cum valorile „NA” se aliniază la sfârșit. Ca parametru nostru na.last = True a fost adevărat.
b) Seq: generează o secvență a numărului între două numere specificate.
Sintaxă
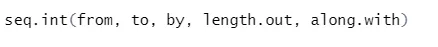
Iată explicația parametrilor săi:
- de la, la început și la sfârșitul valorii secvenței.
- după: Creștere / decalaj între două numere consecutive în succesiune
- lungime.out: lungimea necesară a secvenței.
- Along.with: Se referă la lungimea de la lungimea acestui argument
Cod R și ieșire:
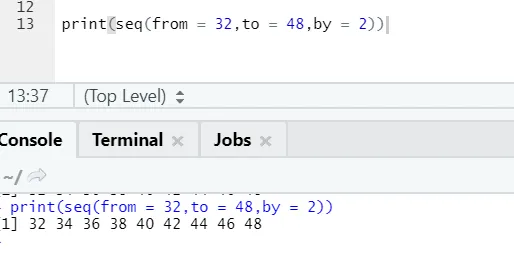
Aici se poate observa că secvența generată are o creștere de 2, deoarece prin este definit ca 2.
c) Toupper, tolower: Cele două funcții: toupper și tolower sunt funcții aplicate pe șir pentru a schimba cazurile literelor din propoziții.
Cod R și ieșire:
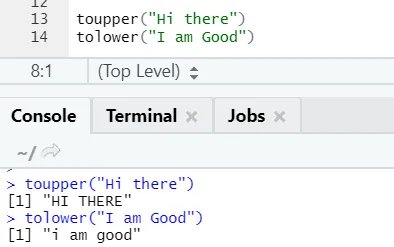
Se poate observa cum se schimbă cazurile de litere atunci când sunt aplicate funcției.
d) Rnorm: Aceasta este o funcție încorporată care generează numere aleatorii.
Cod R și ieșire:
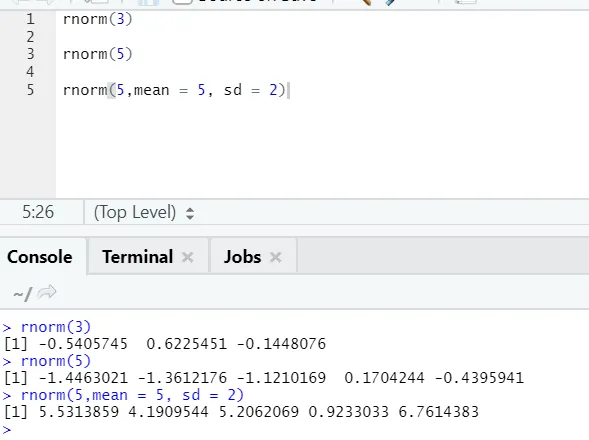
Funcția rnorm ia primul argument care spune câte numere trebuie să fie generate.
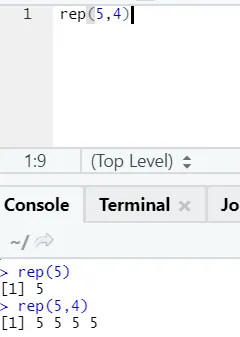
e) Rep: Această funcție reproduce valoarea de câte ori este specificat.
Sintaxa R: rnorm (x, n)
Aici x reprezintă valoarea de replicat, iar n reprezintă numărul de ori care trebuie replicat.
Cod R și ieșire:
f) Lipire: Această funcție este de a concatena șiruri împreună cu un anumit caracter specific între ele.
sintaxă
paste(x, sep = “”, collapse = NULL)
Cod R
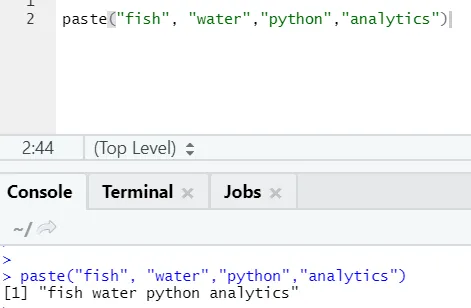
paste("fish", "water", sep=" - ")
Ieșire R:
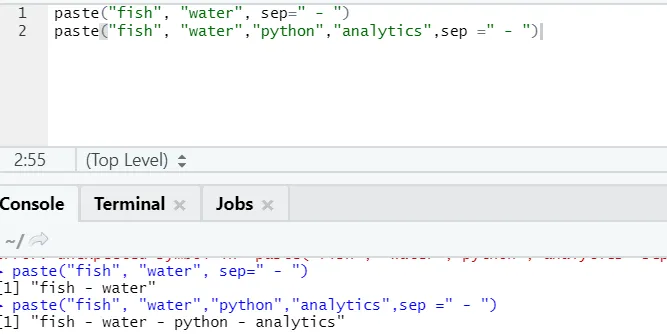
După cum vedeți, putem lipi și mai mult de două șiruri. Sep este acel personaj specific pe care l-am adăugat între șiruri. În mod implicit, sep este spațiu.
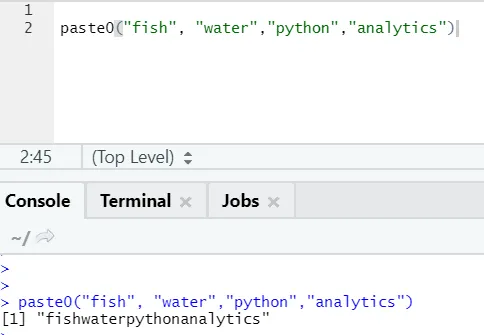
O altă funcție similară există ca aceasta, de care toată lumea ar trebui să fie conștientă este pasta0.
Funcția paste0 (x, y, collapse) funcționează similar cu pasta (x, y, sep = "", colaps)
Vedeți exemplul de mai jos:
În cuvinte simple, pentru a rezuma pasta și pasta0:
Paste0 este mai rapid decât pasta atunci când vine vorba de concatenarea șirurilor fără niciun separator. Întrucât pasta caută întotdeauna „sep” și care este spațiu în mod implicit în ea.
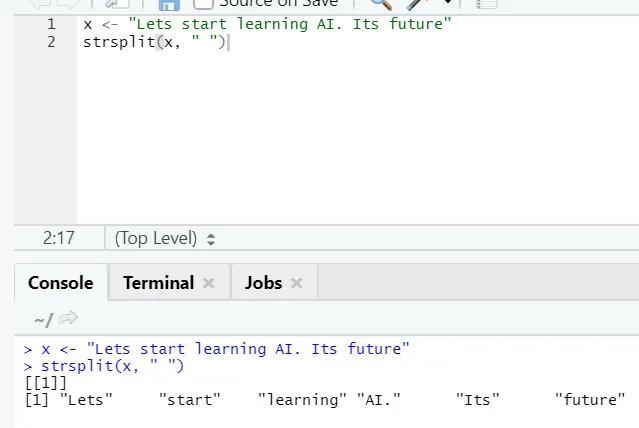
g) Strsplit: Această funcție este de a împărți șirul. Să vedem cazurile simple:
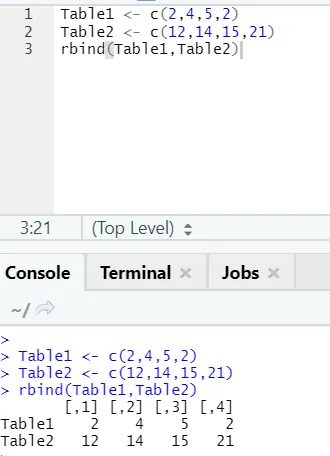
h) Rbind: funcția rbind ajută la combaterea vectorilor cu același număr de coloane, una peste alta.
Exemplu
i) cbind: Aceasta combină vectorii cu același număr de rânduri, una lângă alta.
Exemplu
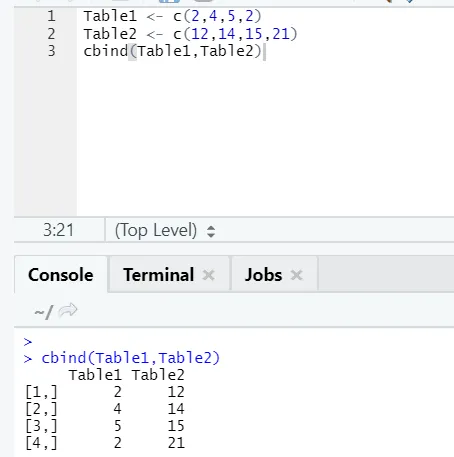
În cazul în care numărul de rânduri nu se potrivește, mai jos este eroarea pe care o veți găsi:

Atât cbind cât și rbind ajută la manipularea și remodelarea datelor.
2) Funcția matematică -
R oferă o mare varietate de funcții matematice. Să vedem câteva dintre ele în detaliu:
a) Sqrt: Această funcție calculează rădăcina pătrată a unui număr sau a unui vector numeric.
Cod R și ieșire:
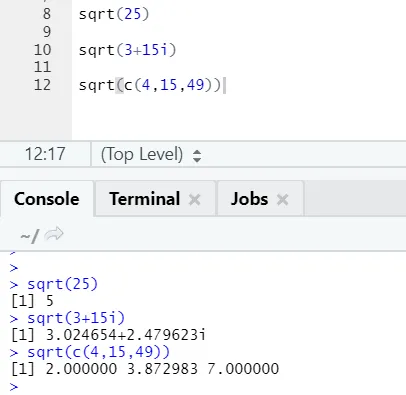
Se poate vedea cum se poate calcula rădăcina pătrată a unui număr, a unui număr complex și a unei secvențe de vector numeric.
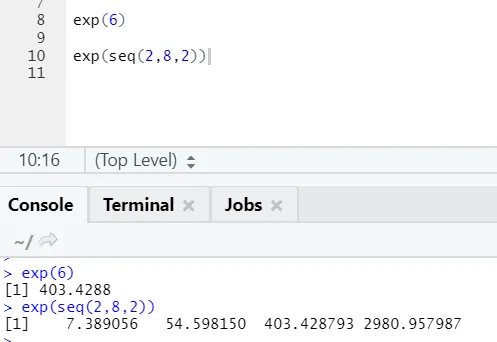
b) Exp: Această funcție calculează valoarea exponențială a unui număr sau a unui vector numeric.
Cod R și ieșire:
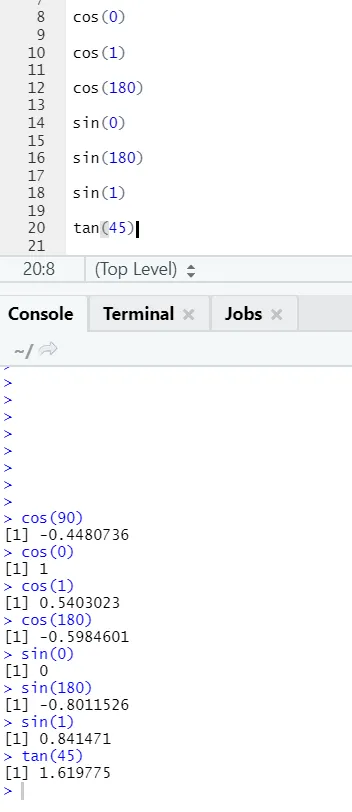
c) Cos, Sin, Tan: Acestea sunt funcții de trigonometrie implementate în R aici.
Cod R și ieșire:
d) Abs: Această funcție returnează valoarea absolută pozitivă a unui număr.
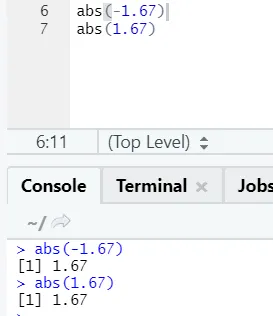
După cum puteți vedea, negativul sau pozitivul unui număr va fi returnat în forma sa absolută. Să o vedem pentru un număr complex:
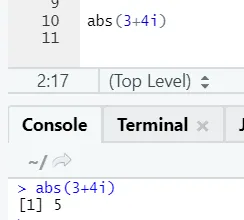
e) Jurnal: Acesta este pentru a găsi logaritmul unui număr.
Iată exemplul prezentat mai jos:
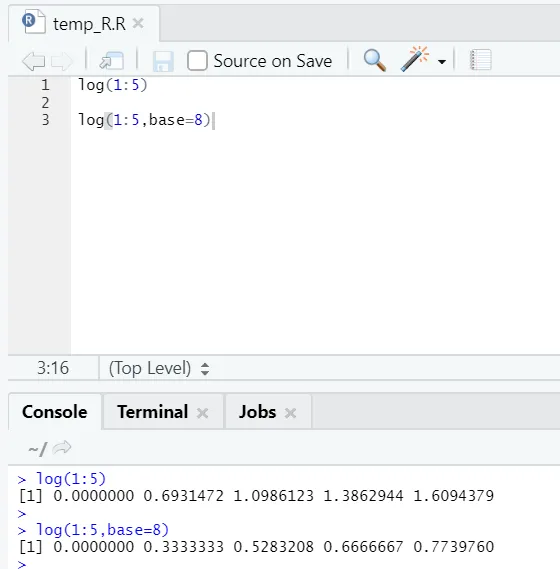
Aici se obține flexibilitate pentru a schimba baza, conform cerințelor.
f) Cumsum: Aceasta este o funcție matematică care dă sume cumulate. Iată exemplul de mai jos:
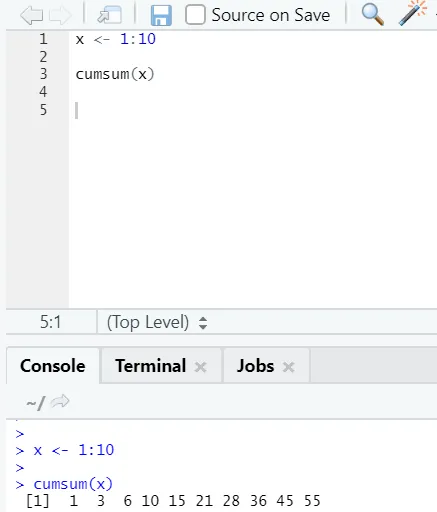
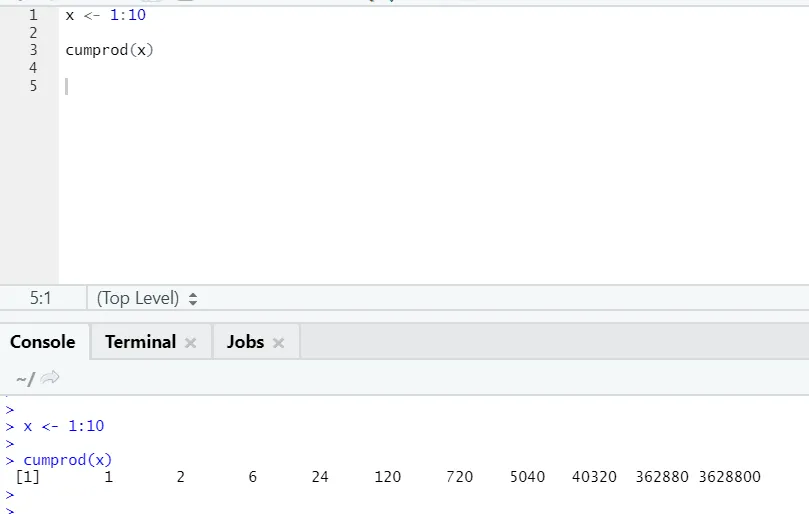
g) Cumprod: Ca funcția matematică Cumsum, avem cumprod unde se înmulțește cumulativ.
Vedeți exemplul de mai jos:
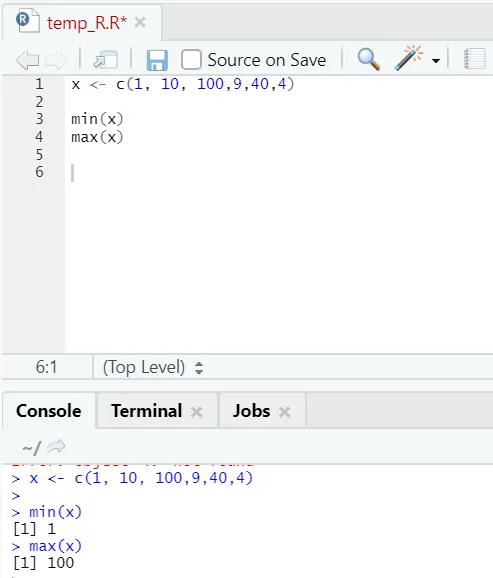
h) Max, Min: Acest lucru vă va ajuta să găsiți valoarea maximă / minimă în setul de numere. Vezi mai jos exemplele legate de acest lucru:
i) Plafonul: plafonul este o funcție matematică care returnează cel mai mic din numărul întreg mai mare decât cel specificat.
Să arătăm un exemplu:
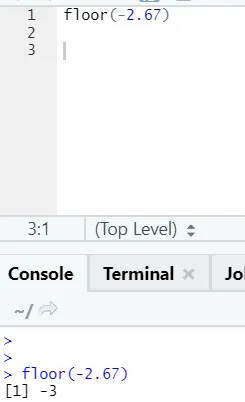
plafon (2.67)
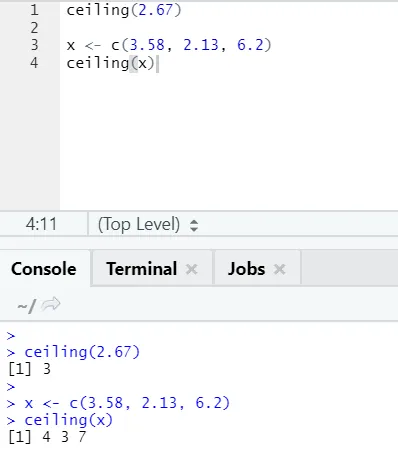
După cum puteți observa, plafonul este aplicat peste un număr, precum și peste o listă, iar ieșirea a venit este cea mai mică din următorul număr întreg.
j) Etaj: Etajul este o funcție matematică care returnează valoarea minimă a numărului specificat.
Exemplul prezentat mai jos vă va ajuta să înțelegeți mai bine:
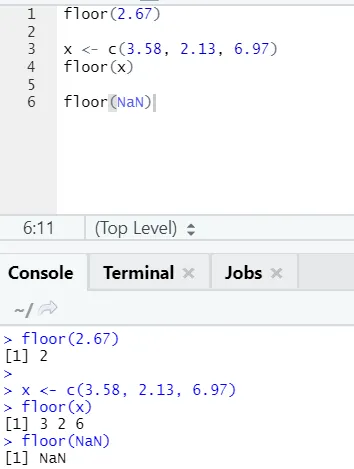
Acționează în același mod și pentru valori negative. Te rog uita-te:
3) Funcții statistice -
Acestea sunt funcțiile care descriu distribuția probabilității aferente.
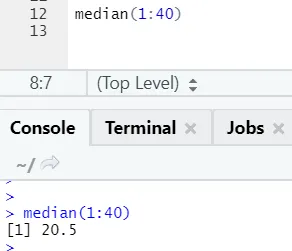
a) Mediana: Aceasta a calculat mediana din succesiunea numerelor.
Sintaxă
Cod R și ieșire:
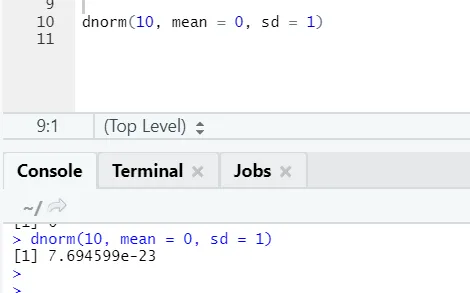
b) Dnorm: Aceasta se referă la distribuția normală. Funcția dnorm returnează valoarea funcției densității probabilității, pentru distribuția normală a parametrilor dați pentru x, μ și σ.
Cod R și ieșire:
c) Cov: Covarianța spune dacă doi vectori sunt neafectați pozitiv, negativ sau total.
Cod R
x_new = c(1., 5.5, 7.8, 4.2, -2.7, -5.5, 8.9)
y_new = c(0.1, 2.0, 0.8, -4.2, 2.7, -9.4, -1.9)
cov(x_new, y_new)
Ieșire R:
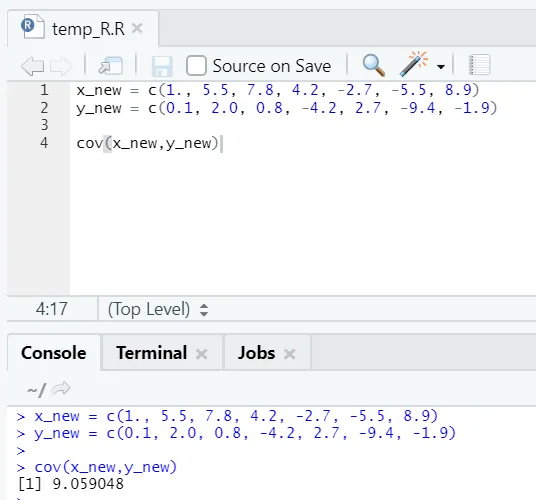
După cum puteți vedea, doi vectori sunt înrudiți pozitiv, ceea ce înseamnă că ambii vectori se mișcă în aceeași direcție. Dacă covarianța este negativă, înseamnă că x și y sunt invers legate și, prin urmare, se deplasează în direcția opusă.
d) Cor: Aceasta este o funcție pentru a găsi corelația dintre vectori. Dă de fapt factorul de asociere între cei doi vectori, care este cunoscut sub numele de „coeficientul de corelație”. Corelația adaugă un factor de grad peste covarianță. Dacă doi vectori sunt corelați pozitiv, corelația vă va spune, de asemenea, cu cât de extinse sunt înrudite pozitiv.
Aceste trei tipuri de metode care pot fi utilizate pentru a găsi o corelație între doi vectori:
- Corelația Pearson
- Corelație Kendall
- Corelația Spearman
În format R simplu, arată:
cor(x, y, method = c("pearson", "kendall", "spearman"))
Aici x și y sunt vectori.
Să vedem exemplul practic de corelație asupra unui set de date încorporat.
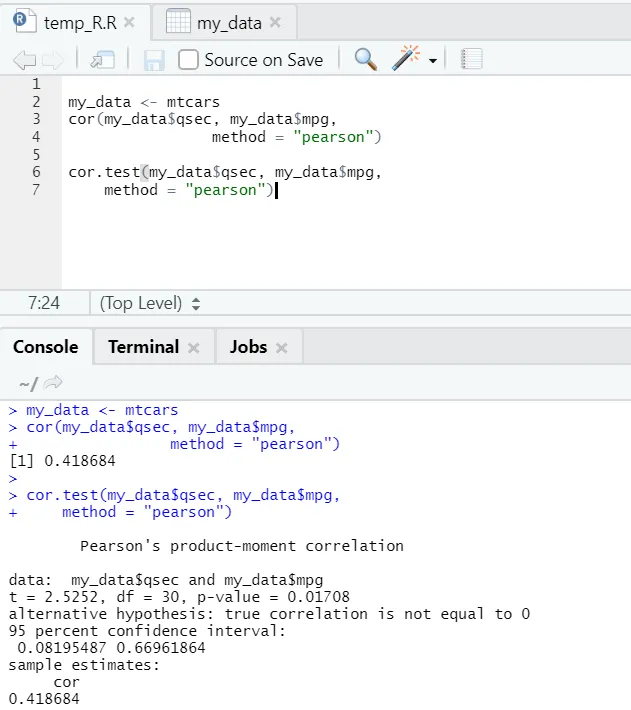
Așadar, aici puteți vedea funcția „cor ()” a dat coeficientul de corelație 0.41 între „qsec” și „mpg”. Cu toate acestea, o altă funcție a fost, de asemenea, prezentat, adică „cor.test ()”, care nu numai că indică coeficientul de corelație, ci și valoarea p și valoarea t legată de acesta. Interpretarea devine mult mai ușoară cu funcția cor.test.
Similar se poate face cu celelalte două metode de corelație:
Codul R pentru metoda Pearson:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = " pearson ")
cor.test(my_data$qsec, my_data$mpg, method = " pearson")
Codul R pentru metoda Kendall:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = " kendall")
cor.test(my_data$qsec, my_data$mpg, method = " kendall")
Codul R pentru metoda Spearman:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = "spearman")
cor.test(my_data$qsec, my_data$mpg, method = "spearman")
Coeficientul de corelație este cuprins între -1 și 1.
Dacă coeficientul de corelație este negativ, asta implică când x crește y scade.
Dacă coeficientul de corelație este zero, asta presupune că nu există nicio asociere între x și y.
Dacă coeficientul de corelație este pozitiv, asta înseamnă că atunci când x crește y tinde să crească.
e) Test T: Testul T vă va spune dacă două seturi de date provin din aceeași distribuție (presupunând) sau nu.
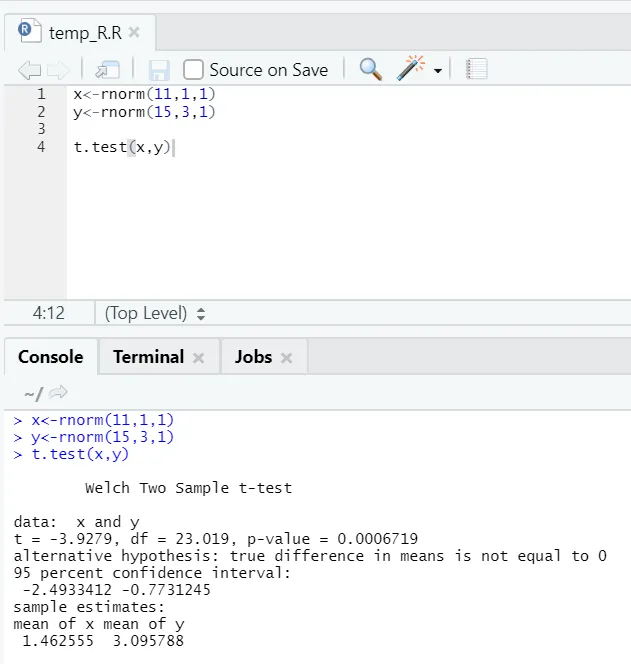
Aici ar trebui să respingi ipoteza nulă conform căreia cele două mijloace sunt egale deoarece valoarea p este mai mică de 0, 05.
Această instanță arătată este de tip: seturi de date nepereche cu variații inegale. În mod similar, poate fi încercat cu setul de date pereche.
f) Regresie liniară simplă: Aceasta arată relația dintre predictor / variabilă independentă și răspuns / dependentă.
Un exemplu practic simplu ar putea fi prezicerea greutății unei persoane dacă se cunoaște înălțimea.
R sintaxa
lm(formula, data)
Aici formula prezintă relația dintre ieșire, ie și variabila de intrare iex Datele reprezintă setul de date, pe care formula trebuie să fie aplicată.
Să vedem un exemplu practic, în care suprafața etajului este variabila de intrare și chiria este variabila de ieșire.
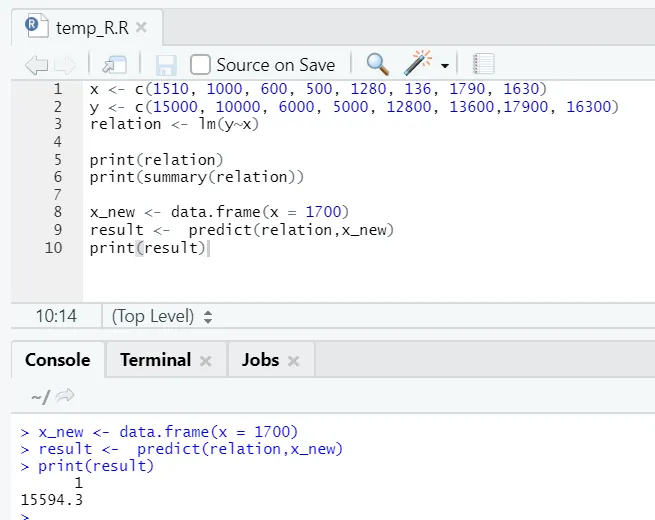
x <- c (1510, 1000, 600, 500, 1280, 136, 1790, 1630)
y <- c (15000, 10000, 6000, 5000, 12800, 13600, 17900, 16300)
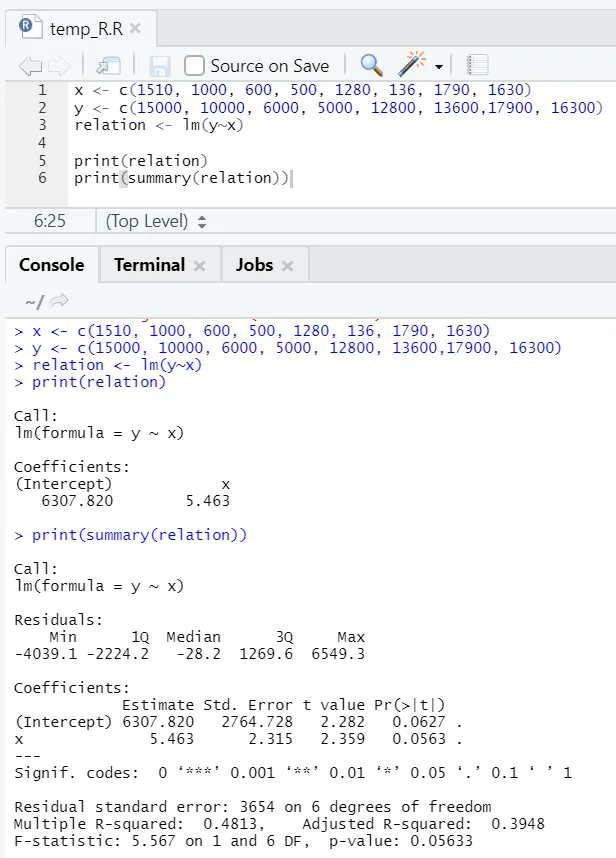
Aici valoarea P nu este mai mică de 5%. Prin urmare, ipoteza nulă nu poate fi respinsă. Nu există prea multă semnificație pentru a dovedi relația dintre suprafața etajului și chirie.
Aici valoarea R-pătrat este 0, 4813. Aceasta implică doar 48% din variația variabilei de ieșire poate fi explicată de variabila de intrare.
Să spunem acum că trebuie să prezicem pentru o valoare a suprafeței de pardoseală, pe baza modelului prevăzut mai sus.
Cod R
x_new <- data.frame(x = 1700)
result <- predict(relation, x_new)
print(result)
Ieșire R:
După executarea codului R de mai sus, ieșirea va arăta astfel:
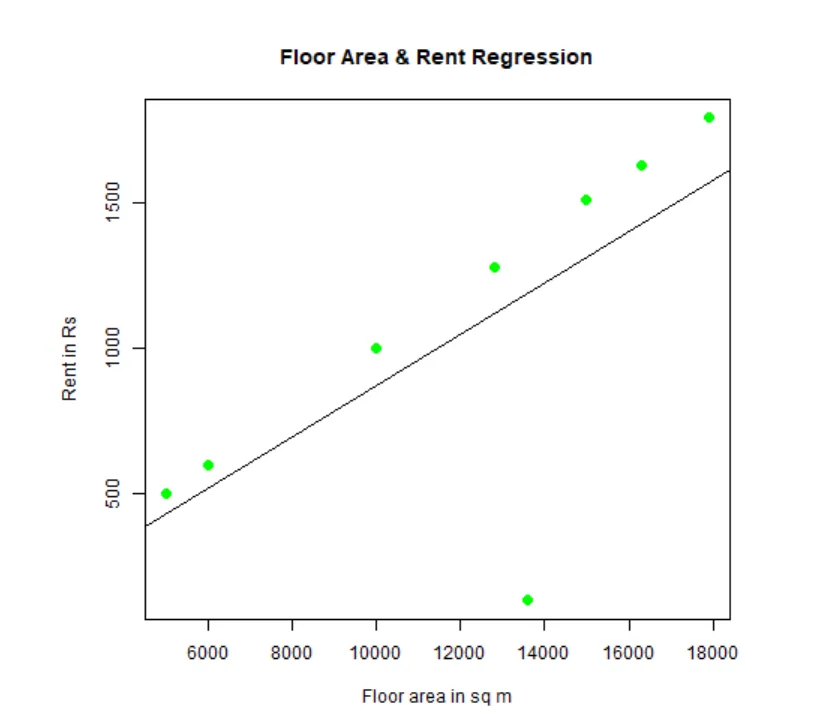
Se poate potrivi și vizualiza regresia. Iată codul R pentru asta:
# Dați unui nume fișierului grafic png.
png(file = "LinearRegressionSample.png.webp")
# Diagrama graficului.
plot(y, x, col = "green", main = "Floor Area & Rent Regression",
abline(lm(x~y)), cex = 1.3, pch = 16, xlab = "Floor area in sq m", ylab = "Rent in Rs")
# Salvați fișierul.
dev.off()
Acest grafic „LinearRegressionSample.png.webp” va fi generat în directorul dvs. de lucru actual.
g) Testul Chi-Square
Aceasta este o funcție statistică în R. Acest test își păstrează semnificația pentru a demonstra dacă există corelație între două variabile categorice.
Acest test funcționează de asemenea ca orice alte teste statistice s-au bazat pe valoarea p, se poate accepta sau respinge ipoteza nulă.
R sintaxa
chisq.test(data), /code>
Să vedem un exemplu practic al acesteia.
Cod R
# Încărcați biblioteca.
library(datasets)
data(iris)
# Creați un cadru de date din setul principal de date.
iris.data <- data.frame(iris$Sepal.Length, iris$Sepal.Width)
# Creați un tabel cu variabilele necesare.
iris.data = table(iris$Sepal.Length, iris$Sepal.Width)
print(iris.data)
# Efectuați testul Chi-Square.
print(chisq.test(iris.data))
Ieșire R:
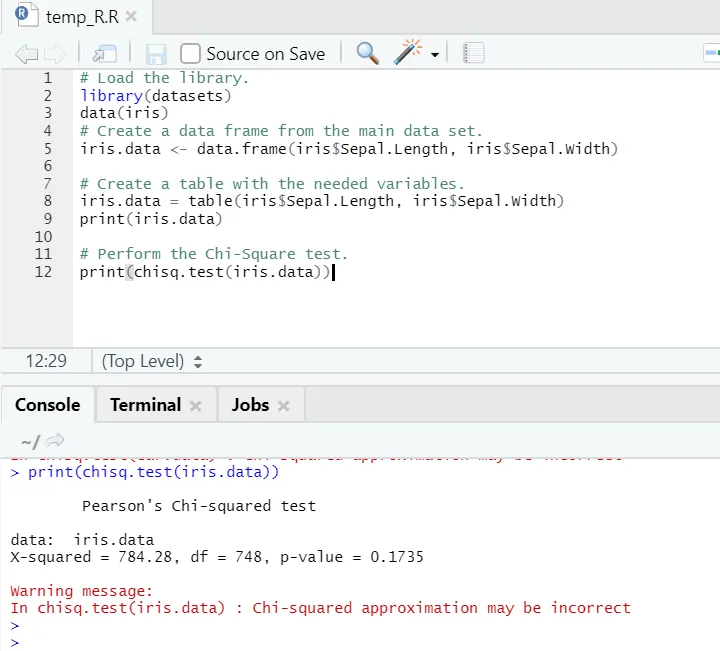
După cum se poate vedea, testul chi-pătrat a fost efectuat pe un set de date iris, având în vedere cele două variabile ale sale „Sepal. Lungime ”și„ Sepal.Width ”.
Valoarea p nu este mai mică de 0, 05, prin urmare nu există o corelație între aceste două variabile. Sau putem spune că aceste două variabile nu depind unele de altele.
Concluzie
Funcțiile în R sunt simple, ușor de montat, ușor de înțeles și totuși foarte puternice. Am văzut o varietate de funcții care sunt folosite ca parte a elementelor de bază în R. Odată ce unul se simte confortabil cu aceste funcții discutate mai sus, se pot explora alte varietăți de funcții. Funcțiile vă ajută, faceți ca codul dvs. să funcționeze simplu și într-un mod concis. Funcțiile pot fi încorporate sau definite de utilizator, totul depinde de necesitate în timp ce abordează o problemă. Funcțiile dau o formă bună unui program.
Articole recomandate
Acesta este un ghid pentru Funcții în R. aici discutăm cum se scrie Funcții în R și diferite tipuri de Funcții în R cu sintaxă și exemple. De asemenea, puteți consulta articolul următor pentru a afla mai multe -
- Funcții cu șiruri R
- Funcții cu șiruri SQL
- T-SQL Funcții șir SQL
- Funcții cu șiruri PostgreSQL