Introducere la sortarea haldei în C
Sortarea este o tehnică care se referă la ordonarea elementelor pe baza diferitelor proprietăți. (Proprietăți precum aranjarea datelor în ordine ascendentă, descendentă sau alfabetică). Un exemplu major de sortare la care ne putem gândi aici este comandarea articolelor în timpul cumpărăturilor online. Ne putem raporta la prețuri, popularitate, cele mai recente și așa mai departe. Deci există multe tehnici pentru această poziționare a elementelor prin sortare. În acest subiect, vom afla despre Sortul haldei în C.
Aici vom învăța una dintre cele mai comune tehnici de sortare, Heap Sort, prin limbajul de programare C.
Logica pentru Heap Sort
Cum de fapt putem efectua un fel de morman? Să vedem mai jos.
În primul rând, grămada este una dintre structurile de date bazate pe arbori. Arborele implicat aici este întotdeauna un Arbore binar complet. Și, există două feluri de grămadă
- Min - Heap: dispusă în general în ordine crescătoare, adică în cazul în care elementul nod parent are o valoare mai mică decât cea a elementelor nodului copil.
- Max - Heap: dispusă în general în ordine descrescătoare, adică în cazul în care elementul nod parent are o valoare mai mare decât cea a elementelor nodului copil.
Pași pentru sortarea haldei
- Odată obținute date de listă nesortate, elementele sunt organizate în structura de date heap, fie pe baza creării unui min-heap sau a unui max-heap.
- Primul element din lista de mai sus este adăugat în tabloul nostru
- Din nou formarea tehnicii de structură a datelor de la cap la fel ca primul pas este urmată și din nou fie cel mai înalt element, fie cel mai puțin element este ridicat și adăugat în tabloul nostru.
- Pașii repetiți ne ajută să obținem tabloul cu lista sortată.
Program pentru sortarea haldei în C
#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)
În primul rând, solicităm utilizatorului să introducă numărul de elemente care sunt luate pentru sortare și apoi utilizatorului i se permite să introducă diferite elemente care urmează să fie sortate.
Pașii urmați
- Următorul lucru pe care ne concentrăm este să creăm un tablou de grămezi, în acest caz, matricea max-heap.
- Principala condiție pentru obținerea unui tablou max - heap este să verificați dacă nicio valoare a nodului părinte nu este mai mică decât valoarea nodului copil. Vom schimba până vom atinge această condiție.
- Avantajul principal în acest arbore binar complet este că nodurile copil stânga și dreapta ale unui nod părinte pot fi accesate cu valorile 2 (i) + 1 și respectiv 2 * (i) + 2. Unde sunt nodul părinte.
- Așadar, prin acest mod aici, plasăm nodul nostru rădăcină care conține valoarea maximă în locul nodului frunzei din dreapta. Și apoi din nou urmând aceeași procedură, astfel încât următorul număr maxim devine acum nodul rădăcină.
- Vom urma aceeași procedură până când un singur nod nu va rămâne în tabloul de grădină.
- Și apoi, ne aranjăm tabloul de grămadă pentru a forma un tablou sortat perfect în ordine crescătoare.
- În cele din urmă, imprimăm tabloul sortat în ieșire.
ieşire:
Produsul este atașat mai jos.
Permiteți-mi să vă arăt reprezentarea picturală a întâmplărilor:
- Datele introduse sunt reprezentate pentru prima dată sub forma unui tablou unidimensional după cum urmează.

- Reprezentarea picturală a arborelui binar format este următoarea:
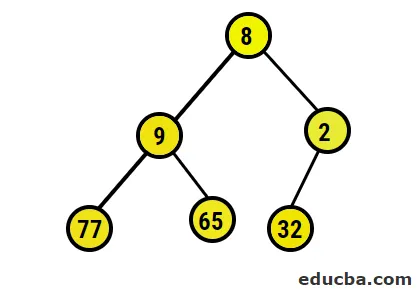
- Acum, vom converti la maximul de asigurări, asigurându-ne că toate nodurile părinte sunt întotdeauna mai mari decât nodurile copil. Așa cum s-a menționat în ieșirea sub un tablou sortat la grămadă, reprezentarea picturală ar fi:
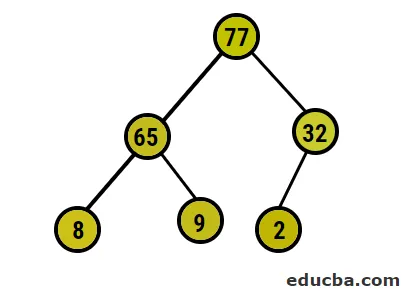
- După aceasta, vom schimba nodul rădăcină cu nodul extrem al frunzei și apoi îl vom șterge din copac. Nodul frunzei ar fi rădăcina acum și din nou același proces e urmat pentru a obține din nou cel mai înalt element din rădăcină
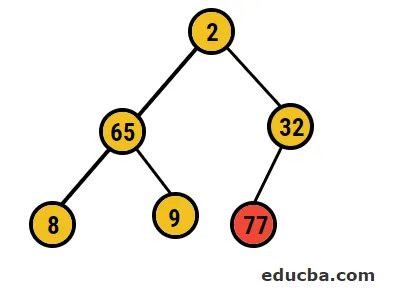
- Deci, în acest caz, 77 de cifre sunt șterse din acest arbore și introduse în tabloul nostru sortat și procesul se repetă.
Cele de mai sus am văzut-o pentru formarea tabloului de adunare maximă. Același proces este tratat și cu formarea tabloului min-heap. După cum am discutat mai sus, singura diferență este relația dintre elementele nodului părinte și copil.
Ca exercițiu, puteți încerca să formați sortul de morman în ordinea descrescătoare?
Concluzie
Deși există numeroase tehnici de sortare, sortarea haldelor este considerată una dintre cele mai bune tehnici de sortare din cauza complexității sale de timp și spațiu. Complexitatea de timp pentru toate cele mai bune, medii și cele mai rele cazuri este O (nlogn), unde complexitatea cazurilor cele mai rele este mai bună decât complexitatea cazurilor cele mai grave ale lui Quicksort și complexitatea spațială este O (1).
Articole recomandate
Acesta este un ghid pentru Heap Sort în C. Aici vom discuta despre logica și pașii pentru sortarea hamei cu codul și ieșirea eșantionului împreună cu reprezentările picturale. De asemenea, puteți arunca o privire la următoarele articole pentru a afla mai multe -
- Sortare la grămadă în Java
- Sortare selecție în Java
- Palindrom în programul C
- Modele în programarea C
- Sortare la grămadă în C ++ (Algoritm)
- Sort de grămadă în Python
- C Înmulțirea matricei de programare