
Introducere în distribuția binomială în R
Acest articol descrie modul de utilizare a distribuțiilor binomiale în R pentru puținele operații implicate cu distribuțiile de probabilitate. Analiza de afaceri folosește probabilitatea binomială pentru o problemă complexă. R are numeroase funcții încorporate pentru calculul distribuțiilor binomiale utilizate în interferențele statistice. Distribuția binomială cunoscută și sub denumirea de încercări Bernoulli are două tipuri de succes p și eșec S. Obiectivul principal al modelului de distribuție binomială este acela de a calcula rezultatele probabilității posibile prin monitorizarea unui număr specific de posibilități pozitive, prin repetarea procesului de un anumit număr de ori . Acestea ar trebui să aibă două rezultate posibile (succes / eșec), prin urmare rezultatul este dihotom. Notarea matematică predefinită este p = succes, q = 1-p.
Există patru funcții asociate distribuțiilor binomiale. Sunt dbinom, pbinom, qbinom, rbinom. Sintaxa formatată este dată mai jos:
Sintaxă
- dbinom (x, dimensiune, prob)
- pbinom (x, dimensiune, prob)
- qbinom (x, dimensiune, prob) sau qbinom (x, dimensiune, prob, low_tail, log_p)
- rbinom (x, dimensiune, prob)
Funcția are trei argumente: valoarea x este un vector al cuantilelor (de la 0 la n), dimensiunea este numărul de încercări de trasee, probă indică probabilitatea pentru fiecare încercare. Să vedem unul câte unul cu un exemplu.
1) dbinom ()
Este o funcție de densitate sau de distribuție. Valorile vectorului trebuie să fie un număr întreg nu trebuie să fie un număr negativ. Această funcție încearcă să găsească un număr de succes într-un nr. a încercărilor fixate.
O distribuție binomială are dimensiuni și valori x. de exemplu, mărimea = 6, valorile x posibile sunt 0, 1, 2, 3, 4, 5, 6 ceea ce implică P (X = x).
n <- 6; p<- 0.6; x <- 0:n
dbinom(x, n, p)
ieşire:
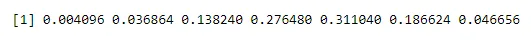
Crearea probabilității unuia
n <- 6; p<- 0.6; x <- 0:n
sum(dbinom(x, n, p))
ieşire:
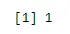
Exemplul 1 - Baza de date a spitalului arată că pacienții care suferă de cancer, 65% mor din cauza acestuia. Care este probabilitatea ca 5 pacienți aleși la întâmplare din care 3 să se recupereze?
Aici aplicăm funcția dbinom. Probabilitatea ca 3 să se recupereze folosind distribuția densității în toate punctele.
n = 5, p = 0, 65, x = 3
dbinom(3, size=5, prob=0.65)
ieşire:

Pentru valoarea x de la 0 la 3:
dbinom(0, size=5, prob=0.65) +
+ dbinom(1, size=5, prob=0.65) +
+ dbinom(2, size=5, prob=0.65) +
+ dbinom(3, size=5, prob=0.65)
ieşire:
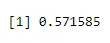
În continuare, creați un eșantion de 40 de lucrări și incrementați cu 2 creând și binomial folosind dbinom.
a <- seq(0, 40, by = 2)
b <- dbinom(a, 40, 0.4)
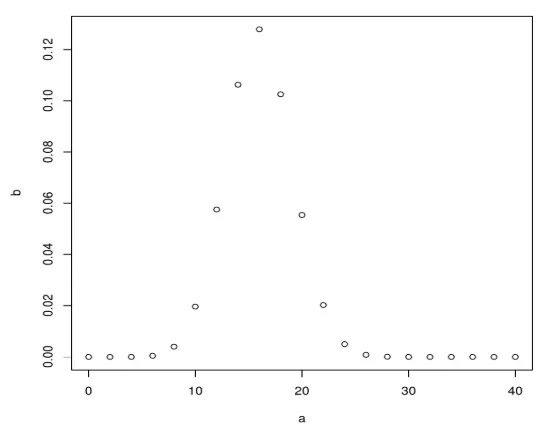
plot(a, b)
Produce următoarea ieșire după executarea codului de mai sus, Distribuția binomială este reprezentată folosind funcția plot ().
Exemplul 2 - Luați în considerare un scenariu, să presupunem că probabilitatea ca un student să împrumute o carte dintr-o bibliotecă este 0, 7. Există 6 studenți în bibliotecă, care este probabilitatea ca 3 dintre ei să împrumute o carte?
aici P (X = 3)
Cod:
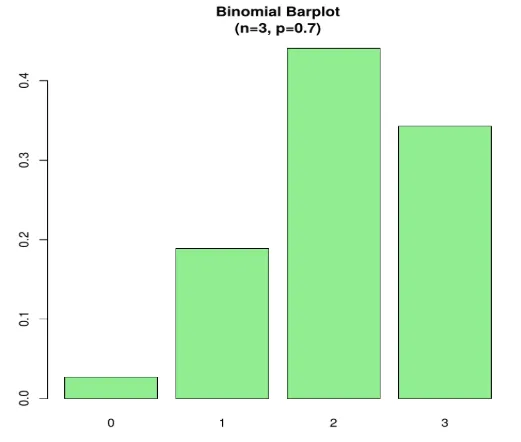
n=3; p=.7; x=0:n; prob=dbinom(x, n, p);
barplot(prob, names.arg = x, main="Binomial Barplot\n(n=3, p=0.7)", col="lightgreen")
Mai jos Plot arată când p> 0, 5, prin urmare distribuția binomială este înclinată pozitiv, așa cum este afișat.
ieşire:
2) Pbinom ()
calculează probabilități cumulate ale binomului sau CDF (P (X <= x)).
Exemplul 1:
x <- c(0, 2, 5, 7, 8, 12, 13)
pbinom(x, size=20, prob=.2)
ieşire:

Exemplul 2: Dravid marchează o răchită la 20% din încercările sale atunci când se învârte. Dacă ar fi bol de 5 ori, care ar fi probabilitatea ca acesta să înscrie 4 sau mai puțin wicket?
Probabilitatea succesului este de 0, 2 aici și pe parcursul a 5 încercări
pbinom(4, size=5, prob=.2)
ieşire:
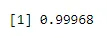
Exemplul 3: 4% dintre americani sunt negri. Găsiți probabilitatea a 2 studenți negri când selectați la întâmplare 6 studenți dintr-o clasă de 100, fără înlocuire.
Când R: x = 4 R: n = 6 R: p = 0. 0 4
pbinom(4, 6, 0.04)
Ieșire: -
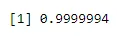
3) qbinom ()
Este o funcție cuantică și inversează funcția de probabilitate cumulată. Valoarea cumulată se potrivește cu o valoare de probabilitate.
Exemplu: Câte cozi vor avea o probabilitate de 0, 2 atunci când o monedă este aruncată de 61 de ori.
a <- qbinom(0.2, 61, 1/2)
print(a)
Ieșire: -
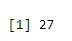
4) rbinom ()
Generează numere aleatorii. Rezultate diferite produc rezultate aleatorii diferite, utilizate în procesul de simulare.
Exemplu:-
rbinom(30, 5, 0.5)
rbinom(30, 5, 0.5)
Ieșire: -

De fiecare dată când îl executăm dă rezultate aleatorii.
rbinom(200, 4, 0.4)
Ieșire: -

Aici facem acest lucru presupunând rezultatul a 30 de flipuri de monedă într-o singură încercare.
rbinom(30, 1, 0.5)
Ieșire: -
Folosind barplot:
a<-rbinom(30, 1, 0.5)
print(a)
barplot(table(a),>
Ieșire: -
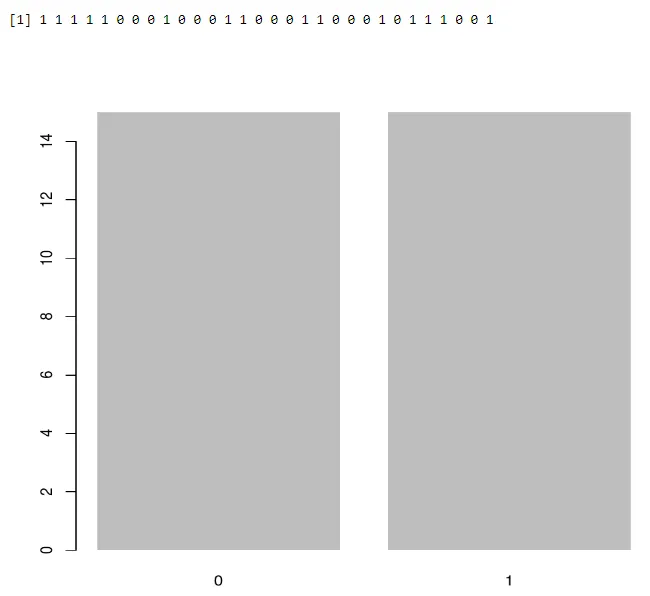
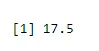
Pentru a găsi mijlocul succesului
output <-rbinom(10, size=60, 0.3)
mean(output)
Ieșire: -
Concluzie - Distribuția binomială în R
Prin urmare, în acest document am discutat despre distribuția binomială în R. Am simulat folosind diferite exemple în R studio și în fragmentele R și am descris, de asemenea, funcțiile încorporate ajută la generarea calculelor binomiale. Calculul distribuției binomiale în R utilizează calcule statistice. Prin urmare, o distribuție binomială ajută la găsirea probabilității și la căutarea aleatorie folosind o variabilă binomială.
Articole recomandate
Acesta este un ghid pentru distribuția binomială în R. Aici am discutat o introducere și funcțiile sale asociate cu distribuția binomială împreună cu sintaxa și exemple adecvate. Puteți parcurge și alte articole sugerate pentru a afla mai multe -
- Formula binomială de distribuție
- Economie vs afaceri
- Tehnici de analiză de afaceri
- Distribuții Linux