
Diferența dintre scorul Z față de scorul T
Scorul Z este o conversie a datelor brute la un scor standard, când conversia se bazează pe media populației și pe abaterea standard a populației. Când un set complet de date este disponibil la noi, putem calcula scorul Z. Scorul Z este scăderea mediei populației de la scorul brut și apoi împarte rezultatul cu abaterea standard a populației. Scorul T este o conversie a datelor brute la scorul standard atunci când conversia se bazează pe media eșantionului și pe deviația standard a eșantionului. Atunci când setul de date privind populația nu este disponibil, atunci trebuie să colectăm câteva exemple de date pentru a calcula media eșantionului și abaterea standard a populației.
Scorul Z
În cadrul unei distribuții normale, unde sunt disponibile date complete, aceasta se află la o distanță față de medie. Formula sa este cea prezentată mai jos,
Z= (x-μ)/σ
Unde,
X = date brute individuale
μ = Media populației
σ = abaterea standard a populației
Scorul T
Scorul T este scăderea abaterii standard individuale de la media individuală și apoi divizează rezultatul cu deviația standard a eșantionului rezultat întreg înmulțit cu dimensiunea eșantionului. Formula sa este cea prezentată mai jos,
t = ((- μ)/s)*
= Exemplu mediu
μ = Media populației
s = Exemplu Abatere standard
n = dimensiunea eșantionului
Să luăm un exemplu pentru a înțelege același lucru într-o manieră mai bună:
Într-o lucrare, există trei subdiviziuni - I, II și III. Numărul studenților care au răspuns I va fi corect 25%, adică 75% nu pot răspunde corect. În mod similar, lăsați 10% și 20% din numărul de persoane care au răspuns corect la secțiunile II și III, astfel 90% și 80% au găsit secțiunea II și III. Presupunem că abilitatea măsurată de aceste trei elemente este aceeași și este distribuită în mod normal,
Scorul pentru fiecare elev dintr-o clasă este utilizat pentru a calcula media notelor care este egală cu 50 și o abatere standard de 10. Putem calcula scorul Z cu scorul de 50 ca (50-50) / 10 = 0
Putem interpreta că scorul studentului este 0 distanță (în unități de abateri standard) față de medie, deci elevul a obținut media.
Dacă scorul este 60, scorul Z este (60-50) / 10 = 1
Putem interpreta că elevul a marcat peste medie - o distanță de 1 abatere standard peste medie.
Comparație față în față între scorul Z și scorul T (Infografie)
Mai jos este diferența de top 9 dintre scorul Z față de scorul T 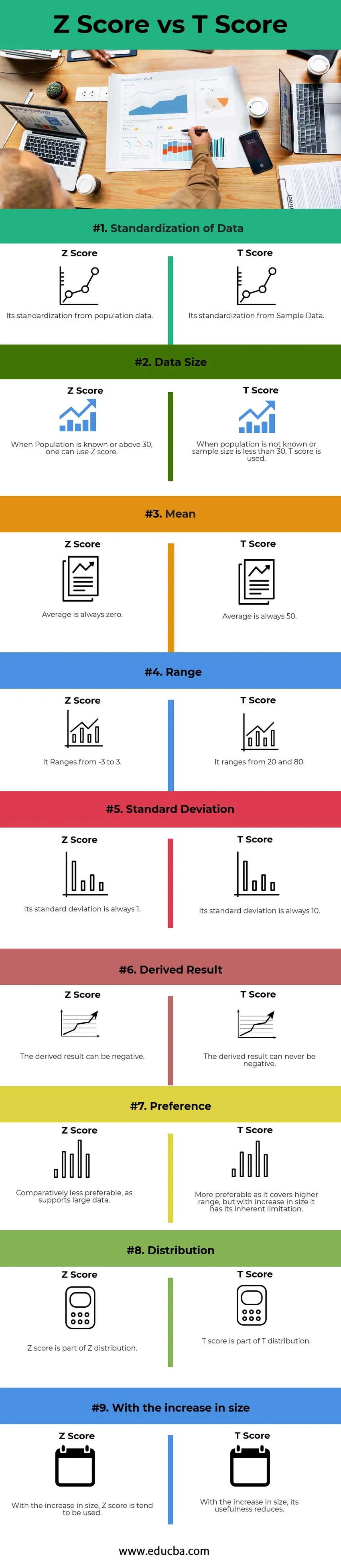
Diferențe cheie între scorul Z față de scorul T
Să discutăm unele dintre diferențele majore între scorul Z față de scorul T
- Scorul Z este standardizarea de la datele brute ale populației sau mai mult de 30 de date de eșantion la scorul standard, în timp ce scorul T este standardizarea de la datele de eșantion de mai puțin de 30 de date la scorul standard
- Scorul Z variază de la -3 la 3, în timp ce scorul T variază de la 20 la 80.
- Pe măsură ce dimensiunea datelor crește, distribuția tinde să fie distribuția Z. Atât distribuția scorului Z, cât și a scorului T face parte dintr-o distribuție normală, dar în funcție de dimensiunea diferă între ele
- Practic, scorul Z este utilizat pe scară largă în datele pieței bursiere și pentru a verifica șansele ca o companie să intre în faliment, în timp ce t scorul este utilizat pe scară largă pentru verificarea densității mineralelor osoase și a evaluărilor riscului de fractură.
Scorul Z față de scorul T Tabelul comparativ
Să ne uităm la top 9 Comparație între scorul Z și scorul T
| Sr. Nu. | Puncte de comparație | Scorul Z | Scorul T |
| 1 | Standardizarea datelor | Standardizarea sa din datele privind populația | Standardizarea sa din Exemple de date |
| 2 | Dimensiunea datelor | Când populația este cunoscută sau peste 30, se poate utiliza scorul Z | Când populația nu este cunoscută sau dimensiunea eșantionului este mai mică de 30, se utilizează scorul T. |
| 3 | Rău | O medie este întotdeauna zero. | O medie este întotdeauna 50. |
| 4 | Gamă | Acesta variază de la -3 la 3. | Acesta variază între 20 și 80. |
| 5 | Deviație standard | Abaterea sa standard este întotdeauna 1 | Abaterea sa standard este întotdeauna 10 |
| 6 | Rezultat derivat | Rezultatul derivat poate fi negativ | Rezultatul derivat nu poate fi niciodată negativ |
| 7 | Preferinţă | Comparativ mai puțin de preferat, deoarece acceptă date mari | Mai preferabil, deoarece acoperă o gamă mai mare, dar cu o creștere a dimensiunii, are limitarea sa inerentă |
| 8 | distribuire | Scorul Z face parte din distribuția Z | Scorul T face parte din distribuția T |
| 9 | Odată cu creșterea dimensiunii | Odată cu creșterea dimensiunii, scorul Z tinde să fie utilizat | Odată cu creșterea dimensiunilor, utilitatea acestuia se reduce. |
Concluzie
Atât scorul Z, cât și scorul T face parte din testarea ipotezelor în condițiile unei distribuții normale. Dacă aveți un set de scoruri de măsurare pe diferite măsuri folosind scoruri Z, puteți spune cum sunt plasate scorurile în distribuțiile lor. Atunci le poți compara. Standardizarea scorurilor este o procedură utilizată pe scară largă în domeniul cercetării și planificării, deoarece acestea ajută la compararea diferitelor scoruri de test. Standardizarea scorurilor înainte de combinarea lor ajută un cercetător să obțină rezultate mai bune și comparabile.
Articole recomandate
Acesta a fost un ghid pentru diferența maximă între scorul Z față de scorul T. Aici vom discuta, de asemenea, diferențele cheie de scor Z față de scorul T cu infografie și tabelul de comparație. De asemenea, puteți arunca o privire la următoarele articole pentru a afla mai multe-
- Finanțe vs economie - diferență de top
- Deficit vs datorii - Care este mai bun
- Achiziție de active și cumpărare de acțiuni
- Piața monetară și piața de capital
- Prezentare generală a scorului Altman Z