Introducere în algoritmul de clustering ierarhic
Algoritmul ierarhic de clustering este o tehnică de învățare automată nesupravegheată. Acesta urmărește găsirea unui grup natural bazat pe caracteristicile datelor.
Algoritmul de clustering ierarhic are ca scop găsirea grupurilor imbricate de date prin construirea ierarhiei. Este similară cu taxonomia biologică a regnului vegetal sau animal. Grupurile ierarhice sunt în general reprezentate folosind arborele ierarhic cunoscut sub numele de dendrogramă.
Tipuri de algoritm de ierarhizare a grupării
Algoritmii de clustering ierarhici sunt de 2 tipuri:
- discordie
- aglomerativ
1. Diviziv
Aceasta este o abordare de sus în jos, în care inițial consideră datele întregi ca un singur grup, apoi divizează în mod iterativ datele în subgrupuri. Dacă se cunoaște numărul unui algoritm de ierarhizare a grupării, atunci procesul de divizare se oprește odată ce numărul de clustere este obținut. Altfel, procesul se oprește atunci când datele nu mai pot fi împărțite, ceea ce înseamnă că subgrupa obținută din iterația curentă este aceeași cu cea obținută din iterația anterioară (se poate considera, de asemenea, că diviziunea se oprește atunci când fiecare punct de date este un cluster. ).
2. aglomerativ
Este o abordare de jos în sus, care se bazează pe fuziunea grupurilor. Inițial, datele sunt împărțite în m grupuri singleton (unde valoarea lui m este numărul de eșantioane / puncte de date). Două clustere sunt îmbinate într-un singur iterativ, reducând astfel numărul de clustere în fiecare iterație. Acest proces de fuziune a clusterelor se oprește atunci când toate grupurile au fost îmbinate într-unul sau numărul de clustere dorit.
La nivelul 1, există m grupuri care se reduc la 1 cluster la nivelul m. Punctele de date care se îmbină pentru a forma un cluster la un nivel mai mic rămân în același cluster și la nivelurile superioare. De exemplu, să presupunem că există 8 puncte x1..x8, deci, inițial, există 8 grupuri la nivelul 1. Să presupunem că punctele x1 și x2 sunt îmbinate într-un cluster la nivelul 2, apoi până la nivelul 8, acestea rămân în același grup.
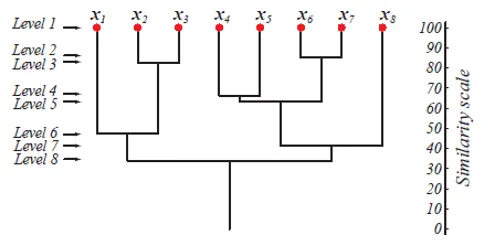
Figura de mai sus arată o reprezentare a dendrogramei abordării de aglomerare de aglomerare pentru 8 puncte de date, precum și scara de similaritate corespunzătoare fiecărui nivel.
Nivelurile clusterelor ne oferă o idee despre cât de similare sunt punctele de date din clustere. Așa cum se arată în fig. 1, punctele de date devin contopite într-un cluster, acestea sunt similare. Deci, punctele de date dintr-un cluster la nivelul 2 (de exemplu, x2 și x3) sunt mai similare decât acele puncte de date dintr-un cluster la nivelul 6 (de exemplu, x1 și x2).
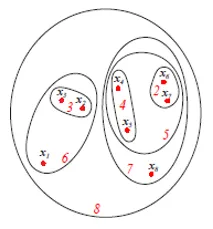
Figura de mai sus prezintă reprezentarea diagramei Set sau Venn a abordării aglomerative de grupare a celor 8 puncte de date menționate mai sus. Atât dendrogramele cât și reprezentările setate pot fi utilizate pentru clustering. Cu toate acestea, o dendrogramă este de obicei de preferat reprezentarea activului nu poate reprezenta cantitativ asemănările clusterului.
Pași pentru algoritmul de agregare ierarhică
Să urmăm următorii pași pentru algoritmul ierarhic de clustering care este prezentat mai jos:
1. Algoritm
Algoritmul de aglomerare ierarhică de clustering
- Se începe inițializarea c, c1 = n, Di = (xi), i = 1, …, n '
- Faceți c1 = c1 - 1
- Găsiți cele mai apropiate clustere, să zicem, Di și Dj
- Merge Di și Dj
- Până c = c1
- Întoarceți ciorchine c
- Sfârșit
Acest algoritm începe cu n clustere inițial unde fiecare punct de date este un cluster. La fiecare iterație, numărul de clustere se reduce cu 1 pe măsură ce cele 2 grupuri cele mai apropiate se îmbină. Acest proces continuă până când numărul de clustere se reduce la valoarea predefinită c.
Cum să decidem ce clustere sunt în apropiere?
Aceasta este definită folosind mai multe valori de distanță care sunt următoarele:
- Distanța minimă între clusterele dmin (Di, Dj). Util pentru single.
- Distanța maximă între clusterele dmax (Di, Dj). Util pentru completare.
- Distanța medie între clustere davg (Di, Dj).
Ce este o legătură unică și o legătură completă?
- Când dmin (di, dj) este utilizat pentru a găsi distanța dintre două clustere, iar algoritmul se încheie dacă distanța dintre cele mai apropiate clustere depășește un prag, atunci algoritmul se numește un singur algoritm de legătură.
- Când dmax (Di, Dj) este utilizat pentru a găsi distanța dintre două clustere, iar algoritmul se încheie dacă distanța dintre cele mai apropiate clustere depășește un prag, atunci algoritmul este numit algoritm de legătură completă.
- Să considerăm fiecare punct de date ca un nod al unui grafic. Există o margine între două puncte de date dacă aparțin aceluiași cluster. Când se îmbină două clustere cele mai apropiate, se adaugă o muchie. Se numește o singură legătură, deoarece există o cale unică de la un nod la celălalt.
- Algoritmul complet de legătură combină două clustere prin minimizarea distanței dintre cele două cele mai îndepărtate puncte.
- Un singur algoritm de legătură generează un arbore de acoperire. Cu toate acestea, acest algoritm este susceptibil la zgomot. Un algoritm complet de legătură generează un grafic complet.
Care este complexitatea de timp a algoritmului?
Să presupunem că avem n modele în spațiul d-dimensional și că folosim dmin (Di, Dj) pentru a forma crupuri c. Trebuie să calculăm n (n - 1) distanțe între puncte - fiecare dintre ele fiind un calcul O (d 2 ) - și să plasăm rezultatele într-un tabel de distanță între puncte. Complexitatea spațială este O (n 2 ). Găsirea perechii de distanță minimă (pentru prima contopire) necesită să parcurgem lista completă, păstrând indicele distanței cele mai mici.
Astfel, pentru prima etapă aglomerativă, complexitatea este O (n (n - 1) (d 2 + 1)) = O (n 2 d 2 ). Pentru o altă etapă de aglomerare arbitrară (adică de la c1 la c1 - 1), pur și simplu parcurgem distanțele n (n - 1) - c1 „neutilizate” din listă și găsim cea mai mică pentru care x și x 'se află în diferite grupuri. . Acesta este, din nou, O (n (n − 1) cc1). Complexitatea timpului total este astfel O (cn 2 d 2 ), iar în condiții tipice n >> c.
2. vizualizare
Odată ce datele sunt împărțite în clustere, este o practică bună să vizualizeze clusterele, astfel încât să vă faceți o idee despre cum arată gruparea. Dar vizualizarea acestor date cu dimensiuni înalte este dificilă. Prin urmare, utilizăm Analiza Componentelor Principale (PCA) pentru vizualizare. După PCA, obținem punctele de date în spațiul dimensional redus (în general 2D sau 3D) pe care le putem complota pentru a vedea gruparea.
Notă: dimensiune înaltă înseamnă un număr mare de caracteristici și nu un număr de puncte de date.3. Evaluare
Una dintre metodele de evaluare a clusterelor este aceea că distanța punctelor dintre cluster (distanța dintre cluster) ar trebui să fie mult mai mare decât distanța punctelor din cadrul clusterului (distanța intracluster).
Concluzie
Următoarele sunt câteva dintre primele cheie:
- Algoritmul ierarhic de clustering este utilizat pentru a găsi tipare imbricate în date
- Gruparea ierarhică este de 2 tipuri - divizivă și aglomerativă
- Diagrama și setul / diagrama Venn pot fi utilizate pentru reprezentare
- O singură legătură îmbină două clustere prin minimizarea distanței minime între ele. Formează o întindere
- Legătura completă îmbină două clustere prin minimizarea distanței maxime dintre Formează un grafic complet.
- Complexitatea timpului total al algoritmului ierarhic de clustering este O (cn 2 d 2 ), unde c este numărul predefinit de clustere, n este numărul de tipare și d este spațiul dimensional al n tiparelor.
Articole recomandate
Acesta este un ghid pentru algoritmul de clustering ierarhic. Aici discutăm tipurile și pașii algoritmilor ierarhici de clustering. De asemenea, puteți consulta următoarele articole pentru a afla mai multe-
- Analiza grupării ierarhice
- Gruparea Ierarhică în R '
- Algoritmul de clustering
- Ce este Clustering în Data Mining?
- Gruparea Ierarhică | Gruparea aglomerativă și divizivă
- C ++ Algoritm | Exemple de algoritm C ++