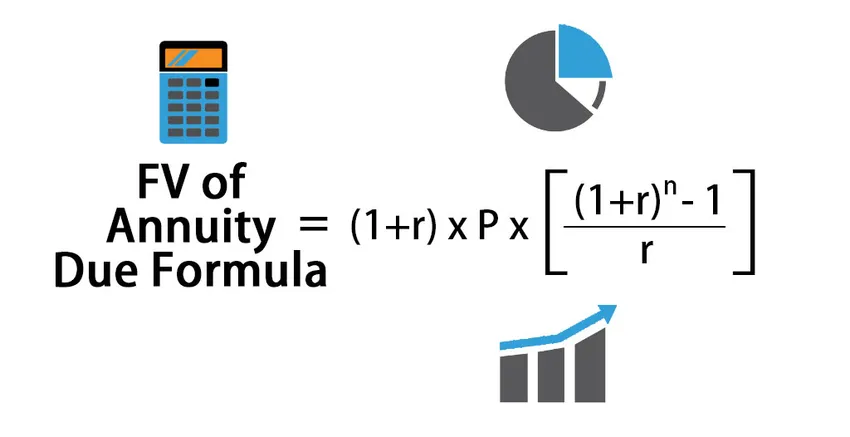
Valoarea viitoare a formulei de rentabilitate datorată (cuprins)
- Valoarea viitoare a formulei de rentabilitate datorată
- Exemple de formulă pentru valoarea viitoare a rentabilității (cu șablonul Excel)
- Valoarea viitoare a calculatorului de formulă datorat anualității
Valoarea viitoare a formulei de rentabilitate datorată
Formula pentru calcularea valorii viitoare a rentabilității datorate:
FV of Annuity Due = (1+r) * P * (((1+r) n – 1) / r )
Unde,
- P = Plata periodică
- R = Rata pe perioadă
- N = numărul de perioade
Exemple de formulă pentru valoarea viitoare a rentabilității (cu șablonul Excel)
Să luăm un exemplu pentru a înțelege calculul valorii viitoare a rentabilității datorate într-o manieră mai bună.
Puteți descărca aici modelul Excel cu formula viitoare a valorii viitoare a Annuity Due - Valoarea viitoare a modelului Excel cu formula Annuity DueExemplul # 1
Să presupunem că un Anand a depus 10.000 USD pe an și rata efectivă pe care o oferă contul său este de 3%. Acum, Anand dorește să își calculeze soldul viitor după 5 ani, asumându-și prima depunere de astăzi înainte.
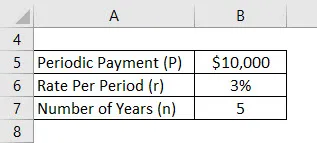
Soluţie:
Valoarea viitoare a rentabilității datorate se calculează folosind formula prezentată mai jos
FV din Annuity Due = (1 + r) * P * (((1 + r) n - 1) / r)
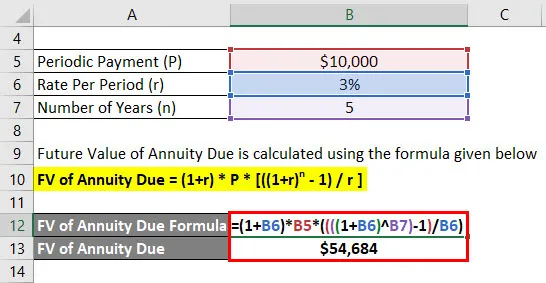
- FV din Annuity Due = (1+ 3%) * 10.000 USD * ((((1 + 3%) 5) - 1) / 3%)
- FV din Annuity Due = 54.684 dolari
Anand va primi 54.684 de dolari soldul viitor după 5 ani.
Exemplul # 2
Să presupunem că un Jagriti a depus 8.000 de dolari pe an, iar rata efectivă pe care o oferă contul său este de 5%. Acum, Jagriti vrea să își calculeze soldul viitor după 5 ani, asumându-și prima depunere de astăzi înainte.

Soluţie:
Valoarea viitoare a rentabilității datorate se calculează folosind formula prezentată mai jos
FV din Annuity Due = (1 + r) * P * (((1 + r) n - 1) / r)
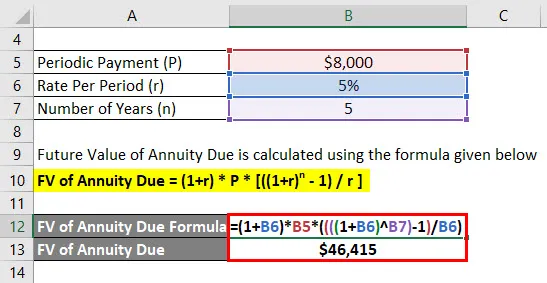
- FV din Annuity Due = (1+ 5%) * 8.000 $ * ((((1 + 5%) 5) - 1) / 5%)
- FV din Annuity Due = 46.415 USD
Jagriti va primi 46.415 dolari soldul viitor după 5 ani.
Exemplul # 3
Să presupunem că un Anandriti a depus 20.000 USD pe an și rata efectivă pe care o oferă contul său este de 2%. Acum, Anandriti vrea să-și calculeze soldul viitor după 5 ani, asumându-și prima depunere de astăzi înainte.
Soluţie:
Valoarea viitoare a rentabilității datorate se calculează folosind formula prezentată mai jos
FV din Annuity Due = (1 + r) * P * (((1 + r) n - 1) / r)
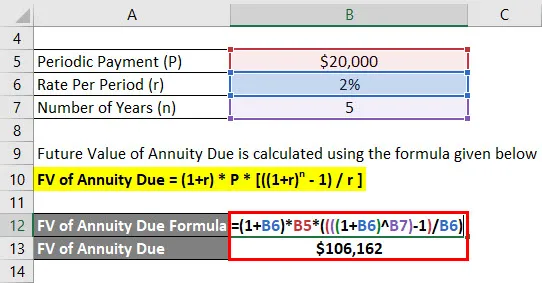
- FV din Annuity Due = (1+ 2%) * 20.000 USD * ((((1 + 2%) 5) - 1) / 2%)
- FV din datoria anuală = 1.06.162 dolari
Anandriti va primi 1.06.162 dolari soldul viitor după 5 ani.
Explicaţie
Pentru a calcula valoarea finală pentru o serie de fluxuri de numerar sau de plată în care prima tranșă este primită instantaneu, folosim Valoarea Viitoare a renta datorată. Prima plată instantanee sau plată distinge anualitatea datorată renta obișnuită. O renta imediata sau instant este denumita o renta datorata.
Calculează valoarea fluxurilor de numerar într-o perioadă viitoare. Utilizarea FV-ului din renta datorată este diferită în situații reale decât valoarea actuală a unei rente datorate. De exemplu, să presupunem că o companie sau o persoană fizică cumpără o rentă și au plătit astăzi prima tranșă. Putem folosi exemplul pentru a explica mai departe, să presupunem că o companie sau o persoană dorește să cumpere o rentă de la oricine și au făcut azi prima plată. Pentru a calcula prețul de plătit în această situație, putem utiliza valoarea actuală a formulei datorate anualității. Cu toate acestea, dacă dorim să calculăm soldul rămas după economisirea dobânzii timp de 5 ani în cont și am decis să achităm prima tranșă astăzi, în acest caz, se utilizează valoarea viitoare a unei rente. Anuitatea datorată poate fi explicată ca un tip de rentă în care fluxurile de numerar apar la începutul fiecărei perioade. Datorită naturii avansate a fluxurilor de numerar, fiecare flux de numerar este supus efectului de compunere pentru fiecare perioadă suplimentară în cazul în care este comparat cu o rentă obișnuită. Valoarea viitoare a unei rente obișnuite este mai mică decât valoarea viitoare a renta, deoarece valoarea viitoare a renta primește o dobândă periodică a factorului unui plus.
Relevanța și utilizările valorii viitoare a rentabilității datorate
Să înțelegem semnificația valorii viitoare și a renta datorată separat. Valoarea viitoare poate fi explicată ca valoarea totală pentru o sumă de numerar care trebuie plătită în viitor la o anumită dată. Și o renta datorată poate fi explicată ca seria de plăți care se face la începutul fiecărei perioade în mod regulat. Prin urmare, valoarea viitoare a renta datorată poate fi explicată ca valoare totală la o dată specificată în viitor pentru o serie de plăți sistematice / periodice în care plățile se efectuează la începutul fiecărei perioade. Acest tip de tranzacție și un astfel de flux de plăți pot fi văzute pentru contul beneficiarului unui plan de pensii. Valoarea totală este suma la care seria de plăți efectuată la data viitoare va crește, deoarece se presupune o anumită sumă de dobândă, iar câștigurile cresc treptat într-o anumită perioadă. Calculul valorii viitoare a unei rente obișnuite este identic cu aceasta, dar singura diferență este că adăugăm o perioadă suplimentară de plată care se face la început.
Valoarea viitoare a calculatorului de formulă datorat anualității
Puteți utiliza următoarea valoare viitoare a calculatoarei anuale datorate
| P | |
| r | |
| n | |
| Valoarea viitoare a formulei de rentabilitate datorată | |
| Valoarea viitoare a formulei de rentabilitate datorată | (1 + r) * P * (((1 + r) n - 1) / r) |
| = | (1 +0) * 0 * (((1 +0) 0 -1) / 0) = 0 |
Articole recomandate
Acesta a fost un ghid pentru Valoarea Viitoare a Formulei Due Annuity. Aici vom discuta despre cum să calculăm Valoarea Viitoare a Annuității Datorită împreună cu exemple practice. Oferim, de asemenea, calculatorul valorii viitoare a Annuity Due cu șablonul Excel descărcabil. De asemenea, puteți consulta următoarele articole pentru a afla mai multe -
- Ghid pentru formula Valoare de bani a timpului
- Exemple de formula actuală a factorului valoric
- Calculator pentru formula raportului de informații
- Formula pentru gradul de levier operațional